Druhá derivace

Druhá derivace je derivace první derivace. U funkce dvou proměnných připadají v úvahu čtyři kombinace. \[ \frac{\partial}{\partial x}\frac{\partial}{\partial x}f,\quad \frac{\partial}{\partial x}\frac{\partial}{\partial y}f,\quad \frac{\partial}{\partial y}\frac{\partial}{\partial x}f,\quad \frac{\partial}{\partial y}\frac{\partial}{\partial y}f. \] Vě většině případů však dvě z těchto derivací splývají, jak ukazuje následující věta.

Věta (Schwarzova).

Jsou-li smíšené derivace hladké na otevřené množině, jsou zde stejné, tj. platí \[ \frac{\partial }{\partial x} \frac{\partial f}{\partial y}= \frac{\partial }{\partial y} \frac{\partial f}{\partial x}.\]

Vzhledem k této větě existují jenom tři druhé parciální derivace. Je tedy bezpečné psát \[ \frac{\partial^2}{\partial x^2}f,\quad \frac{\partial^2}{\partial x \partial y}f,\quad \frac{\partial^2}{\partial y^2}f, \] nebo \[f''_{xx},\quad f''_{xy},\quad f''_{yy}.\]

Totální diferenciál

V aplikacích je jednou za zásadních otázek úloha najít pro dané vektorové pole skalární potenciál, tj. skalární funkci takovou, že gradient této funkce je právě zadané vektorové pole. V některých případech toto je možné, v některých ne. Pokud nějaký skalární potenciál existuje, je studium problému pomocí tohoto potenciálu jednodušší. V notoricky známém případě gravitačního pole tento přístup vede k zavedení pojmu potenciální energie gravitačního pole, který se užívá v mnoha fyzikálních úlohách od středoškolské fyziky dále. V méně známém případě lze například některá proudění (nevírová) popsat pomocí skalárního potenciálu a poté pracovat s odpovídající skalární funkcí, která je sice hůře představitelná než rychlost proudění, narozdíl od rychlosti je však v každém bodě dána pouze jednou hodnotou. To je podstatné odstranění komplikací způsobených vektorovým charakterem pole rychlosti. Jiným příkladem jsou různé modifikace vodního potenciálu užívané při studiu buněk, rostlin nebo vody v půdě.

Za předpokladu dostatečně hladkých funkcí na otevřené množině platí následující věta.

Věta (nutná a postačující podmínka pro existenci potenciálu).

Vektor \[\vec F(x,y) = \left( M(x,y) , N(x,y)\right)\] je gradientem nějaké funkce \(f(x,y)\) právě tehdy když platí \[ \frac{\partial }{\partial y}M(x,y)=\frac{\partial}{\partial x}N(x,y).\]

Totálním diferenciálem funkce \(z=f(x,y)\) v bodě \((x_0, y_0)\) nazýváme výraz \[ \mathrm{d}f= \nabla f (x_0,y_0) \cdot (\mathrm{d}x,\mathrm{d}y)=\frac{\partial f (x_0,y_0)}{\partial x}\mathrm{d}x+\frac{\partial f (x_0,y_0)}{\partial y}\mathrm{d}y. \] Výše uvedená úloha je někdy formulována v pojmech totálního diferenciálu takto: Je dán výraz \[ M(x,y)\mathrm{d}x+N(x,y)\mathrm{d}y,\] rozhodněte, zda je tento výraz totálním diferenciálem. Toto je důležitá otázka ve fyzice, protože umožňuje rozhodnout, ke kterému silovém poli je možno zavést potenciální energii. Funkce \(f\) se v tomto kontextu nazývá skalární potenciál vektorového pole nebo kmenová funkce diferenciálu.

Separace proměnných

Některé funkce dvou proměnných je možno zapsat jako součin dvou funkcí jedné proměnné, například \(\varphi(x,y)=\sin(x^2+1)\frac{\ln y}{y}\). U některých funkcí toto možné není, například funkce \(\varphi(x,y)=x^2-y^2\). Pomocí parciálních derivací je možno podat jednoduchou charakterizaci všech funkcí, majících výše uvedenou vlastnost.

Laplaceův operátor

• Laplaceův operátor \(\Delta\), je definován v kartézských souřadnicích a trojrozměrném prostoru vztahem \[ \Delta f=\frac{\partial^2 }{(\partial x)^2}f+\frac{\partial^2 }{(\partial y)^2}f+\frac{\partial^2 }{(\partial z)^2}f. \] V prostorech jiné dimenze postupujeme analogicky, jenom vynecháme nebo přidáme derivace podle dalších proměnných.
• Označení symbolem \(\Delta\) je stejné jako změna funkce \(f\) a je nutné tyto dva významy symbolu \(\Delta\) nezaměňovat. Chceme-li se vyhnout nedorozumění, je možno pro označení Laplaceova operátoru používat \(\nabla^2\) namísto \(\Delta\).
• Laplaceův operátor vystupuje v problémech týkajících se elektrického nebo gravitačního potenciálu nebo kmitů a šíření vln. Protože Laplaceův operátor je možné získat jako divergenci gradientu, objevuje se tento operátor u difuzní rovnice v homogenním izotropním prostředí s lineární materiálovou odezvou. Toto tedy zahrnuje vedení tepla, proudění vlhkosti nebo proudění tekutin a plynů, včetně úloh spojených podzemní vodou, s ropou a zemním plynem.

Implicitně definovaná funkce

Tečna k vrstevnici

Mějme funkci \(f(x,y)\) dvou proměnných a její vrstevnici na úrovni \(C\) \[f(x,y)=C.\] Tato rovnice za jistých okolností může definovat \(y\) jako funkci proměnné \(x\). Pokusíme se najít derivaci této funkce. K tomu uvažujme bod \((x_0,y_0)\) ležící na této vrstevnici, tj. \(f(x_0,y_0)=C\).

• Rovnice tečné roviny v bodě \((x_0,y_0)\) je \[ z=f(x_0,y_0)+\nabla f(x_0,y_0)\cdot (x-x_0,y-y_0).\]
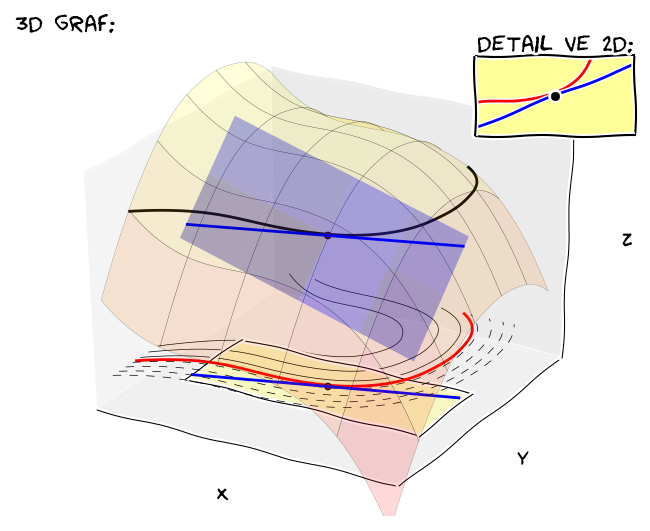
• Řez grafu rovinou \(z=f(x_0,y_0)\) je vrstevnice na úrovni \(C\), řez tečné roviny je tečna k vrstevnici v rovině \(z=C\). Rovnice této tečny je \[ C=f(x_0,y_0)+\nabla f(x_0,y_0)\cdot (x-x_0,y-y_0),\] tj. \[ 0=\nabla f(x_0,y_0)\cdot (x-x_0,y-y_0).\]

Animace

Tečna k vrstevnici

• Normálový vektor tečny je \[ \nabla f(x_0,y_0)=\left(\frac{\partial f (x_0,y_0)} {\partial x}, \frac{\partial f (x_0,y_0)}{\partial y}\right),\] k němu kolmý je vektor \[ \left(-\frac{\partial f (x_0,y_0)}{\partial y}, \frac{\partial f (x_0,y_0)}{\partial x}\right)\] a po znormování první komponenty dostáváme směrový vektor tečny ve tvaru \[ \left(1, -\frac{\frac{\partial f (x_0,y_0)}{\partial x}}{\frac{\partial f (x_0,y_0)}{\partial y}}\right).\] Druhá komponenta tohoto vektoru je derivací funkce, která je dána implicitně rovnicí \[f(x,y)=C.\] To vše za podmínky, že první komponenta normálového vektoru je nenulová.
• Poznámka: bez újmy na obecnosti většinou při definici implicitní funkce bereme \(C=0\). Vskutku, pokud definujeme \(g(x,y)=f(x,y)-C\), potom je možno rovnici vrstevnice funkce \(f\) na úrovni \(C\) přepsat do tvaru \[g(x,y)=0. \]

Věta (o implicitní funkci).

Uvažujme funkci \(f(x,y)\) dvou proměnných, splňující v nějakém bodě \((x_0, y_0)\) podmínku \(f(x_0, y_0)=0\) a mající v okolí bodu \((x_0, y_0)\) spojité parciální derivace. Rovnice \[f(x,y)=0\] vrstevnice na úrovni \(0\) popisuje křivku procházející bodem \((x_0, y_0)\).

• Platí-li \[\frac{\partial f (x_0,y_0)}{\partial y}\neq 0,\] je rovnicí \(f(x,y)=0\) v okolí bodu \((x_0, y_0)\) implicitně určena právě jedna spojitá funkce \(y=g(x)\) (tj. vrstevnice je v okolí bodu \((x_0, y_0)\) grafem nějaké spojité funkce \(g\)).
• Funkce \(g\) z předchozího bodu má v \(x_0\) derivaci \[ g'(x_0)=-\frac{\frac{\partial f (x_0,y_0)}{\partial x}}{\frac{\partial f (x_0,y_0)}{\partial y}}. \]

Extrémy funkce dvou proměnných

Poznámka (tři typy extremálních úloh pro funkce více proměnných).

Předpokládejme, že funkce \(f\) je spojitá a je definována v bodě \((x_0, y_0)\), který je buď vnitřním nebo hraničním bodem definičního oboru. Bude nás zajímat, kdy jsou funkční hodnoty v bodě \((x_0, y_0)\) "co největší", tj. kdy bude platit \[\tag{1} f(x_0, y_0)>f(x,y) \quad\text{pro $(x,y)\neq (x_0, y_0)$}, \] případně, kdy bude platit \[\tag{2} f(x_0, y_0)\geq f(x,y). \] Pokud platí první z nerovností, říkáme, že funkce \(f\) má v bodě \((x_0, y_0)\) ostré maximum a u druhé z nerovností říkáme, že funkce má v bodě \((x_0, y_0)\) neostré maximum. Přitom musíme důkladně specifikovat, co přesně těmito nerovnostmi rozumíme, tj. pro která \((x,y)\) musí nerovnost platit. Tím se budou jednotlivé druhy maxim lišit. V praxi má smysl rozeznávat tři druhy extremálních úloh, které jsou postupně uvedeny v následujících definicích.

Definice (lokální maximum).

Je-li bod \((x_0, y_0)\) vnitřním bodem definičního oboru a nerovnost (1) (případně (2)) platí pro všechna \((x,y)\) z nějakého okolí bodu \((x_0, y_0)\), říkáme, že funkce má v bodě \((x_0, y_0)\) ostré lokální maximum (případně lokální maximum).

Definice (absolutní maximum).

Je-li funkce definovaná na předem zadané množině \(M\) a platí-li nerovnost (1) (případně (2)) pro všechna \((x,y)\in M\), říkáme, že funkce má v bodě \((x_0, y_0)\) ostré absolutní maximum (případně absolutní maximum) na množině \(M\).

Definice (vázané maximum).

Uvažujme další předem zadanou spojitou funkci dvou proměnných \(g:\mathbb{R}^2\to \mathbb{R}\), která splňuje \(g(x_0, y_0)=0\), tj. bod \((x_0, y_0)\) leží na vrstevnici \(g(x,y)=0\) grafu funkce \(g\). Rovnici této vrstevnice \[ g(x,y)=0 \] budeme nazývat vazební podmínkou. Platí-li nerovnost (1) (případně (2)) pro všechna \((x,y)\) z nějakého okolí bodu \((x_0, y_0)\), která splňují vazební podmínku, říkáme, že funkce má v bodě \((x_0,y_0)\) ostré vázané lokální maximum (případně vázané lokální maximum) vzhledem k vazební podmínce (3)}.

Definice (lokální, absolutní a vázané minimum).

Změníme-li směr nerovností (1) a (2), obdržíme podobně (ostré) lokální minimum, (ostré) absolutní minimum na množině \(M\) a (ostré) vázané lokální minimum při vazební podmínce (3).

Věta (absolutní extrémy na kompaktní množině, Weierstrassova věta).

Spojitá funkce má na kompaktní množině absolutní maximum a absolutní minimum.

Poznámka.

Absolutní extrémy jsou buď v bodě, kde je i lokální extrém, nebo na hranici. Ve druhém případě se jedná současně o vázaný extrém, kde vazební podmínkou je hranice. Představme si, že v oblasti hledáme nejvyšší kótu (abosolutní maximum). Nemá smysl hledat uprostřed svahu. Hledáme na vrcholcích kopců, které se v oblasti vyskytují (lokální maximum) a kromě toho má smysl heldat již jen na hranici oblasti (vázaný extrém). Z vazební podmínky jde (alespoň teoreticky) vypočítat jednu proměnnou, dosadit do funkčního předpisu a převést úlohu na hledání lokálního extrému funkce, která má o jednu proměnnou méně. Zbývá problém najít lokální extrémy funkce více proměnných.

Lokální extrémy funkce více proměnných

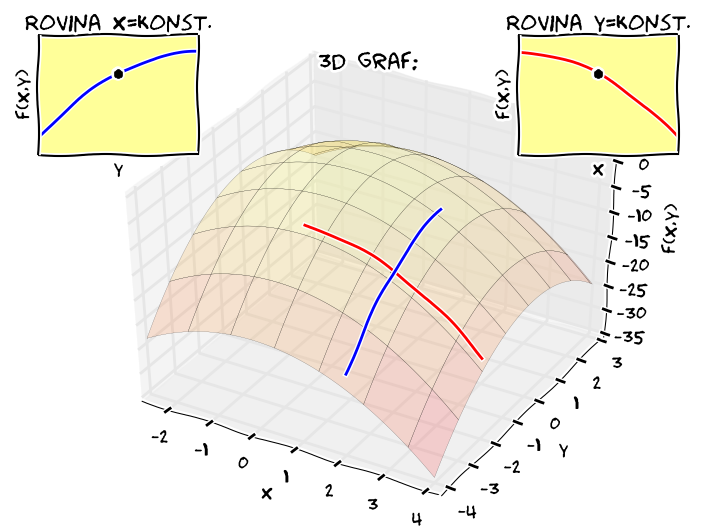
Pokud je některá z parciálních derivací nenulová, extrém nenastává

Slovně vyjádřeno: funkce má v daném bodě lokální minimum, pokud v nějakém okolí tohoto bodu neexistuje bod s menší funkční hodnotou a lokální maximum, pokud v okolí tohoto bodu neexistuje bod s vyšší funkční hodnotou. Pokud v nějakém okolí neexistuje dokonce ani další bod se stejnou funkční hodnotou, nazývají se extrémy ostré lokální minimum a ostré lokální maximum.

Funkce jedné proměnné určitě nemá v bodě lokální extrém, pokud má v tomto bodě kladnou derivaci (protože potom funkce roste), nebo pokud má v tomto bodě zápornou derivaci (protože potom funkce klesá). Derivace v bodě kde nastává lokální extrém tedy musí být buď nulová nebo nesmí existovat. Stejná myšlenková úvaha se dá provést pro křivky vzniklé na řezech funkce dvou proměnných a proto platí následující věta.

Věta (Fermatova nutná podmínka pro lokální extrém).

Jestliže funkce více proměnných má v nějakém bodě svůj lokální extrém, pak každá parciální derivace, která v tomto bodě existuje, je nulová.

Pokud jsou parciálni derivace nulové, extrém ještě nemusí existovat. Bohužel nemáme k dispozici nástroj, pomocí kterého jsme se naučili rozhodovat v případě funkce jedné proměnné -- monotonii. Můžeme ale využít druhé derivace, což je jakási obdoba konvexnosti a konkávnosti funkce.

Věta (dostatečná podmínka pro lokální extrém).

Nechť má funkce \(f\) v bodě \((x_0, y_0)\) obě paricální derivace nulové a nechť funkce jsou obě parciální derivace druhého řádu v okolí tohoto bodu spojité. Označme symbolem \(H\) následující determinant \[ H(x,y)= \begin{vmatrix} \frac{\partial ^2f}{\partial x^2}& \frac{\partial ^2f}{\partial x \partial y}\\ \frac{\partial ^2f}{\partial x \partial y}& \frac{\partial ^2f}{\partial y^2}\\ \end{vmatrix}. \]

Platí-li \(H(x_0,y_0)>0\) a \(\frac{\partial ^2f}{\partial x^2}(x_0,y_0)>0\), má funkce \(f\) v bodě \((x_0, y_0)\) ostré lokální minimum.

Platí-li \(H(x_0,y_0)>0\) a \(\frac{\partial ^2f}{\partial x^2}(x_0,y_0)<0\), má funkce \(f\) v bodě \((x_0, y_0)\) ostré lokální maximum.

Platí-li \(H(x_0,y_0)<0\), potom funkce \(f\) nemá v bodě \((x_0, y_0)\) lokální extrém.

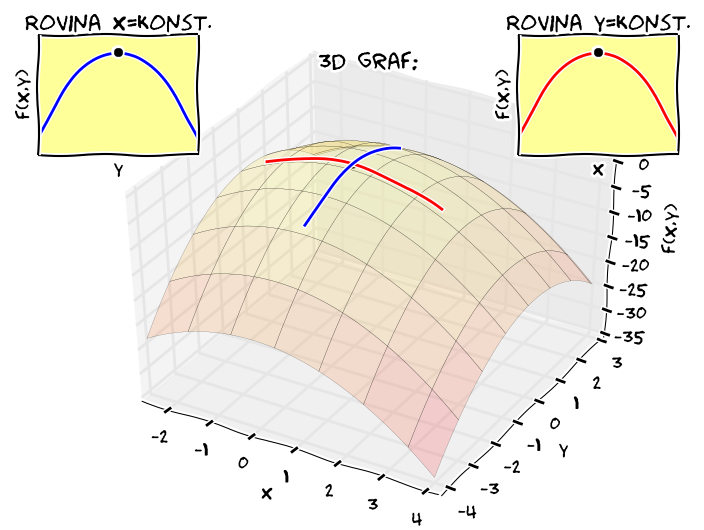
V bodě kde nastává extrém je každá parciální derivace která existuje nulová, tj. křivka na řezu má vodorovnou tečnu

Nulovost parciálních derivací nemusí stačit k existenci lokálního extrému - funkce může mít sedlový bod

Lineární aproximace rovinné transformace

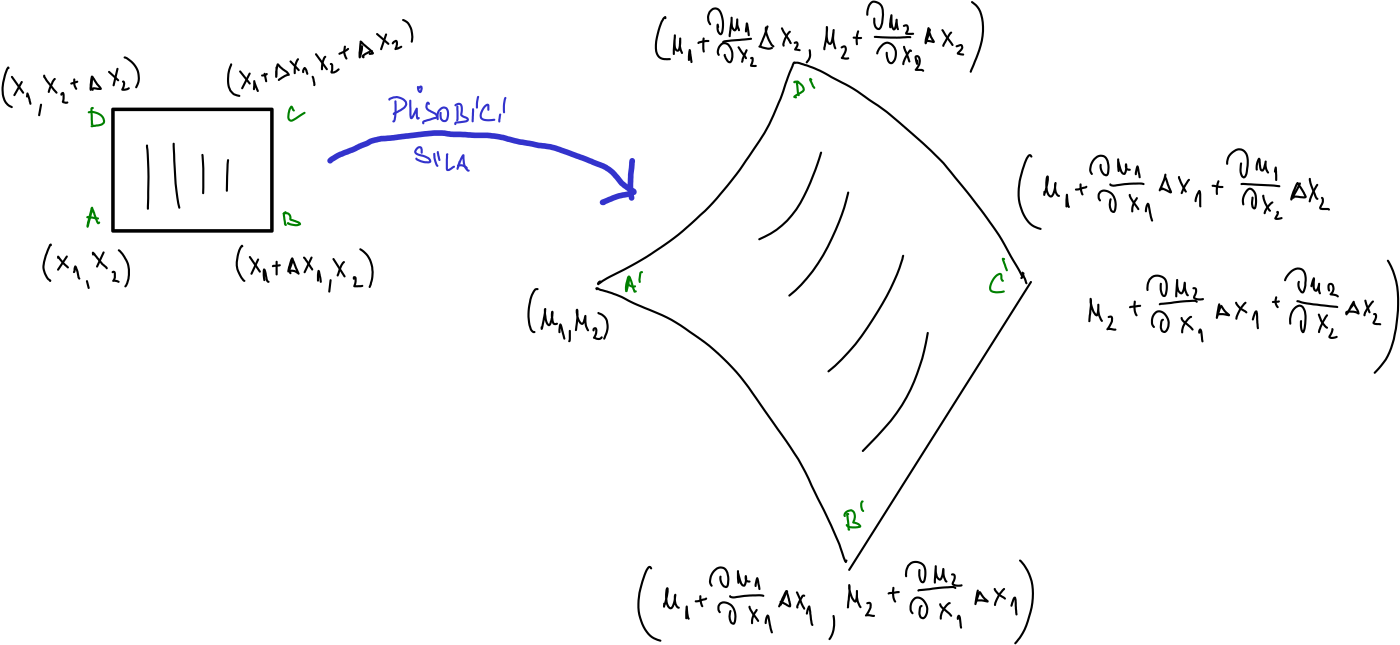
Působením síly se element materiálu může posunout, rotovat, deformovat. Tunto změnu potřebujeme zachytit.

Následující pasáže rozšiřují lineární aproximaci na případ, kdy chceme popsat transformaci roviny. Protože v tomto případě pracujeme se dvěma souřadnicemi, je nutno uvažovat dvě funkce (pro každou souřadnici jednu funkci) a každá funkce závisí na dvou proměnných (na obou souřadnicích). Popis, který si představíme, využijeme při popisu matematického namáhání při odvození veličin, na nichž je založen obecný Hookův zákon dávající do souvislosti deformaci materiálu a působení vnější síly. Používá se v materiálovém inženýrství (deformace dřeva) i v krajinném inženýrství (geologie struktur, structural geology)

Souřadnice v rovině pro pohodlí a pro těsnější souvislost s často používanou literaturou označíme \(x_1\) a \(x_2\). Uvažujme nyní mechanické namáhání, kdy se těleso posunuje, rotuje a deformuje vlivem působení vnější síly a bod \((x_{1}, x_{2})\) se transformuje na bod \((u_{1}(x_{1},x_{2}),u_{2}(x_{1},x_{2})).\) Čtverec \(ABCD\) na obrázku se zobrazí na obrazec \(A'B'C'D'\). Pomocí lineárních aproximací \[ \begin{aligned} u_{1}(x_{1}+\Delta x_{1}, x_{2}+\Delta x_{2})&\approx u_{1}+\frac{\partial u_{1}}{\partial x_{1}}\Delta x_{1}+\frac{\partial u_{1}}{\partial x_{2}}\Delta x_{2}\\ u_{2}(x_{1}+\Delta x_{1}, x_{2}+\Delta x_{2})&\approx u_{2}+\frac{\partial u_{2}}{\partial x_{1}}\Delta x_{1}+\frac{\partial u_{2}}{\partial x_{2}}\Delta x_{2} \end{aligned} \] dostáváme aproximaci polohy bodu \(C'\), založené na relativní poloze bodu \(C\) k \(A\) a na změně polohy bodu \(A\). Tento vztah je možné zapsat maticově jako \[ \begin{pmatrix} u_1 (x_{1}+\Delta x_{1}, x_{2}+\Delta x_{2}) \\ u_1 (x_{1}+\Delta x_{1}, x_{2}+\Delta x_{2}) \end{pmatrix} \approx \begin{pmatrix} u_1\\u_2 \end{pmatrix}+ \begin{pmatrix} \frac{\partial u_{1}}{\partial x_{1}} & \frac{\partial u_{1}}{\partial x_{2}}\\ \frac{\partial u_{2}}{\partial x_{1}} & \frac{\partial u_{2}}{\partial x_{2}} \end{pmatrix} \begin{pmatrix} \Delta x_1 \\ \Delta x_2 \end{pmatrix}. \] Člen \(\begin{pmatrix} u_1\\u_2 \end{pmatrix}\) je posunutí, proto nás zajímá až druhý člen, obsahující deformaci.

Tenzor malých deformací

Metodami lineární algebry kombinovanými s diferenciálním počtem dokážeme ve zobrazení identifikovat tenzor malých deformací, složku související jenom se změnou tvaru. Odfiltrujeme tak posun či rotaci, které se změnou tvaru nesouvisí. Zdroj: pixabay.com

Budeme studovat matici \[D= \begin{pmatrix} \frac{\partial u_{1}}{\partial x_{1}} & \frac{\partial u_{1}}{\partial x_{2}}\\ \frac{\partial u_{2}}{\partial x_{1}} & \frac{\partial u_{2}}{\partial x_{2}} \end{pmatrix} \] z předchozího slidu. Každou matici je možné rozdělit vzorcem \[A=\frac{A+A^T}2 + \frac{A-A^T}2\] na součet symetrické a antisymetrické matice. Pro matici \(D\) dostaneme \[D= \overbrace{\begin{pmatrix} \frac{\partial u_{1}}{\partial x_{1}} & \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}+\frac{\partial u_{2}}{\partial x_{1}}\right)\\ \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}+\frac{\partial u_{2}}{\partial x_{1}}\right)& \frac{\partial u_{2}}{\partial x_{2}} \end{pmatrix} }^{D_{\text{sym}}} + \underbrace{ \begin{pmatrix} 0 & \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}-\frac{\partial u_{2}}{\partial x_{1}}\right)\\ - \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}-\frac{\partial u_{2}}{\partial x_{1}}\right)& 0 \end{pmatrix}}_{D_{\text{asym}}}.\] Druhá část reprezentuje pootočení, což snadno nahlédneme, ji sečteme s identitou, reprezentovanou jednotkovou maticí, na \[ D_{\text{asym}}+I=\begin{pmatrix} 1 & \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}-\frac{\partial u_{2}}{\partial x_{1}}\right)\\ - \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}-\frac{\partial u_{2}}{\partial x_{1}}\right)& 1 \end{pmatrix} \] abychom měli celou část zobrazení (ne jenom deformaci). Porovnáním s maticí malých rotací \[R_{\theta,0}= \begin{pmatrix} 1 & - \theta\\ \theta & 1 \end{pmatrix} \] získáme přímo pootočení. V teorii deformace nás zajímá spíše symetrická část, tj. matice \[ D_{\text{sym}}=\begin{pmatrix} \frac{\partial u_{1}}{\partial x_{1}} & \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}+\frac{\partial u_{2}}{\partial x_{1}}\right)\\ \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}+\frac{\partial u_{2}}{\partial x_{1}}\right)& \frac{\partial u_{2}}{\partial x_{2}} \end{pmatrix} \] popisující změnu tvaru a nazývaná tenzor malých deformací. Ten se ještě někdy rozděluje na součet vhodného konstantního násobku jednotkové matice (souvisí se zvětšením nebo zmenšením, tj. se změnou objemu) a deviátor (souvisí se změnou tvaru bez započtení zvětšení či zmenšení).

Pro využití v dřevařských úlohách viz též A. Požgaj, Štruktúra a vlastnosti dreva str 318 nebo P. Horáček, Fyzikální a mechanické vlastnosti dřeva I, str. 40. Analogicky, ale pro rychlosti, je definován tenzor rychlosti přetvoření (deformační rychlost) používaný v hydrodynamice. Můžeme jej dostat jako derivaci tenzoru malých deformací (při studiu deformací), nebo jako symetrickou část matice vytvořené gradienty jednotlivých komponent rychlosti proudění. Pro proudění vody viz J. Říha, Matematické modelování hydrodynamických a disperzních jevů, kap. 3.3.

Obrázky a online výpočty.

Složené funkce

• Derivace složené funkce \(f(x,y)\), kde \(x=x(u,v)\), \(y=y(u,v)\) je \[\frac {\partial f}{\partial u}=\frac{\partial f}{\partial x} \frac{\partial x}{\partial u}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial u}= \nabla f \cdot \left( \frac{\partial x}{\partial u}, \frac{\partial y}{\partial u}\right).\]
• Derivace složené funkce \(f(x,y,z)\), kde \(x=x(t)\), \(y=y(t)\), \(z=z(t)\) (derivace podél křivky): \[ \frac{\mathrm{d} f}{\mathrm{d} t}=\frac{\partial f}{\partial x}\frac{\mathrm{d} x}{\mathrm{d} t}+\frac{\partial f}{\partial y}\frac{\mathrm{d} y}{\mathrm{d} t}+\frac{\partial f}{\partial z}\frac{\mathrm{d} z}{\mathrm{d} t} = \nabla f \cdot \left(\frac{\mathrm{d} x}{\mathrm{d} t}, \frac{\mathrm{d} y}{\mathrm{d} t}, \frac{\mathrm{d} z}{\mathrm{d} t}\right). \] Je-li křivkou vrstevnice, je \(f\) konstantní podél křivky, derivace je nulová, protože funkční hodnoty se nemění. Skalární součin je nulový a gradient \(\nabla f\) je kolmý na tečný vektor k vrstevnici, tj. na vektor \(\left(\frac{\mathrm{d} x}{\mathrm{d} t}, \frac{\mathrm{d} y}{\mathrm{d} t}, \frac{\mathrm{d} z}{\mathrm{d} t}\right)\).