
Ani přesný vzorec pro vypočítaná data nás nezachrání, pokud je ve vstupních datech nejistota. Pomocí parciálních derivací dokážeme analyzovat, jak moc se výsledek rozmlží vlivem dat zatížených chybou. Zdroj: pixabay.com
Je dán vetknutý nosník na konci zatížený svislou silou \(F\). Deformace nosníku \(\delta\) na konci souvisí (skalární veličina) s velikostí zatěžující síly (skalární veličina). Pro studium problému je vhodné mít převodní pravidlo, které pro každé zatížení udává deformaci. Toto pravidlo bude z matematického úhlu pohledu funkce (funkce jedné proměnné). Může mít například formu \[\delta=\frac 1k F,\] kde \(k\) je konstanta pro daný nosník (tuhost).
Tuhost nosníku závisí na jeho tvaru a fyzikálních charakteristikách. Například pro nosník obdélníkového průřezu délky \(L\), výšky \(h\) a šířky \(w\) může mít tvar \[k=\alpha\frac{w h^3}{L^3},\] kde \(\alpha\) je konstanta pro daný nosník (souvisí s použitým materiálem). Třem nezávislým hodnotám přiřazujeme jednu hodnotu. Toto je funkce tří proměnných.
Letecký radar https://www.flightradar24.com ukazuje aktuální polohu letadel. Každé letadlo, které je ve vzduchu, je v čase \(t\) v místě popsaném dvěma zeměpisnými souřadnicemi. Pro rekonstrukci pohybu můžeme let chápat jako pravidlo, které jedné hodnotě (čas \(t\)) přiřadí dvojici hodnot (souřadnice). Protože tuto dvojici můžeme chápat i jako polohový vektor, nazývá se taková funkce vektorová funkce jedné proměnné.
Meteoradar https://mapy.in-pocasi.cz/ má možnost zobrazit vítr. Každému místu v ČR (popsáno dvěma souřadnicemi, tj. dvourozměrným vektorem) je přidělen dvourozměrný vektor rychlosti větru. Toto je příklad dvourozměrné vektorové funkce dvou proměnných, zkráceně mluvíme o dvourozměrném vektorovém poli.
Pokud chceme zdůraznit, že funkční hodnoty nejsou vektory, nazýváme takové funkce skalární.
Vektorové pole někdy souvisí se skalární funkcí na stejném definičním oboru. Například vítr (vektorová charakteristika) souvisí s tlakem vzduchu v jednotlivých místech (skalární veličina). Podobně piezometrická hladina určuje proudění (Darcyho zákon), rozložení vlhkosti ve dřevě definuje pohyb vody ve dřevě (Fickův zákon), rozložení teploty v materiálu definuje proudění energie (Fourierův zákon). V tomto kontextu se často funkce více proměnných zprostředkovávající vztah mezi oběma veličinami nazývá konstitutivní vztah nebo konstitutivní zákon.
V přednášce o parciálních derivacích jsme se dopustili malého podvodu -- studovali jsme funkce více proměnných aparátem funkcí jedné proměnné. Sledovali jsme změny jenom vzhledem k jedné veličině. Toto někdy nestačí a proto je nutné rozšířit koncept vzdálenosti bodů, otevřených a uzavřených intervalů a spojitosti i pro funkce více proměnných.
Definice (Euklidovský prostor).
Množina \(\mathbb{E}^n\) prvků z \(\mathbb{R}^n\) s metrikou \(\rho\) definovanou pro \(X=(x_1,x_2,\dots x_n)\in\mathbb{R}^n\) a \(Y=(y_1,y_2,\dots, y_n)\in\mathbb{R}^n\) vztahem \[ \label{eq:eukl-metrika} \rho(X,Y)=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+\cdots+(x_n-y_n)^2} \] se nazývá Euklidovský metrický prostor. Prvky prostoru \(E^n\) budeme nazývat body. Funkce \(\rho\) se nazývá Euklidovská metrika. Číslo \(\rho(X,Y)\) se nazývá Euklidovská vzdálenost bodů \(X\), \(Y\).
V prostorech \(\mathbb{E}^2\) a \(\mathbb{E}^3\) se jedná o definici vzdálenosti, používanou v každodenním životě.
Definice (okolí bodu).
Buď \(X\in \mathbb{E}^n\) bod z \(\mathbb{E}^n\) a \(\varepsilon>0\) kladné reálné číslo. Epsilonovým okolím bodu \(X\) rozumíme množinu označenou \(O_\varepsilon(X)\) skládající se z bodů, jejichž vzdálenost od bodu \(X\) je menší než \(\varepsilon\), tj. \[ O_\varepsilon(X)=\{Y\in\mathbb{E}^n:\rho(X,Y)<\varepsilon\}. \] Ryzím epsilonovým okolím bodu \(X\) rozumíme množinu \(\overline O_\varepsilon(X)\) definovanou \[ \overline O_\varepsilon(X)=O_\varepsilon(X)\setminus\{X\}, \] tj. \(\varepsilon\)-okolí bodu \(X\), s vyloučením bodu \(X\).
V diferenciálním počtu funkce jedné proměnné zpravidla studujeme vlastnosti funkcí na intervalech, někdy je podstatná ohraničenost anebo otevřenost/uzavřenost tohoto intervalu. Protože interval je množina bodů mezi dvěma hodnotami, nebývá nutné nijak komentovat vlastnosti intervalů. U vícerozměrných množin je situace pestřejší. Naštěstí dokážeme vyslovit rozšířit všechny pojmy ze světa funkce jedné proměnné do více proměnných tak, že použijeme jenom pojem okolí.
Definice (ohraničená množina).
Množina \(M\) se nazývá ohraničená, jestliže leží v (dostatečně velkém) okolí nějakého bodu \(Y\in\mathbb{E}^n\).
Definice (izolovaný bod a hromadný bod).
Bod \(X\) se nazývá izolovaným bodem množiny \(M\), jestliže existuje okolí \(O(X)\) bodu \(X\) s vlastností \(O(X)\cap M=\{X\}\).
Bod \(X\) se nazývá hromadným bodem množiny \(M\), jestliže každé ryzí okolí bodu \(X\) obsahuje alespoň jeden bod, ležící v množině \(M\).
Definice (vnitřní bod, vnitřek, otevřená množina).
Bod \(X\) se nazývá vnitřním bodem množiny \(M\), jestliže \(X\in M\) a existuje nějaké okolí \(O(X)\) bodu \(X\) ležící celé v množině \(M\), tj. \(O(X)\subseteq M\). Množina všech vnitřních bodů množiny \(M\) se nazývá vnitřek množiny \(M\) a označuje \(M^o\). Je-li množina \(M\) totožná se svým vnitřkem, tj. je-li každý bod množiny \(M\) vnitřní, říkáme, že množina \(M\) je otevřená.
Následující pojem je vícerozměrnou obdobou krajních bodů intervalu.
Definice (hraniční bod a hranice).
Bod \(X\) se nazývá hraničním bodem množiny \(M\), jestliže každé okolí bodu \(X\) obsahuje alespoň jeden bod ležící v množině \(M\) a současně alespoň jeden bod neležící v množině \(M\). Množina všech hraničních bodů množiny \(M\) se nazývá hranice množiny \(M\) a označuje \(\partial M\).
Definice (uzávěr, uzavřená množina).
Uzávěrem množiny \(M\) rozumíme množinu \(\overline M\) definovanou jako sjednocení vnitřku a hranice množiny \(M\), tj. \(\overline M=M^o\cup\partial M\). Je-li množina totožná se svým uzávěrem (tj. obsahuje-li všechny své hraniční body), nazývá se uzavřená.
Definice (souvislá množina).
Množina \(M\) se nazývá souvislá, jestliže každé dva body, ležící v množině \(M\) lze spojit lomenou čarou, ležící v \(M\).
A finále: následující pojmy jsou vícerozměrnou obdobou otevřeného a uzavřeného intervalu.
Definice (oblast, kompaktní množina).
Otevřená souvislá množina se nazývá oblast. Uzavřená souvislá množina se nazývá uzavřená oblast. Uzavřená ohraničená množina se nazývá kompaktní.
Definice (skalární a vektorová funkce více proměnných).
Řekneme, že pravidlo \(f\) je funkcí \(n\) proměnných s definičním oborem \(D(f)\subseteq \mathbb{R}^n\) a oborem hodnot \(Im(f)\subseteq \mathbb{R}^m\), jestliže toto pravidlo každému \(X\in D(f)\) přiřazuje jediný prvek \(Y\in Im(f)\). Píšeme \(Y=f(X)\), prvek \(X\) nazýváme vzor a prvek \(Y\) obraz.
Pro \(m=1\) se funkce \(f\) nazývá skalární funkce, pro \(m>1\) vektorová funkce. Píšeme \(f:\mathbb{R}^n\to\mathbb{R}^m\).
Definice (graf a vrstevnice skalární funkce dvou proměnných).
Uvažujme skalární funkci dvou proměnných \(f:\mathbb{R}^2\to \mathbb{R}\). Grafem funkce \(f\) rozumíme množinu bodů \((x,y,z)\in\mathbb{R}^3\) s vlastností \(z=f(x,y)\).
Nechť \(C\in Im(f)\) je předem dané číslo. Vrstevnicí na úrovni \(C\) rozumíme množinu všech bodů \((x,y)\in\mathbb{R}^2\), splňující \(f(x,y)=C\).
Vizualizace různých typů funkcí.
Grafem funkce dvou proměnných je zpravidla nějaká plocha v prostoru, vrstevnicí zpravidla křivka nebo sjednocení křivek v rovině.
V aplikacích pracujeme zpravidla s vektory dimenze dva nebo tři. Potom vektorové funkce často zapisujeme pomocí jejich komponent ve tvaru \[\vec F(x,y,z)=(P(x,y,z), Q(x,y,z), R(x,y,z)),\] kde \(P\), \(Q\) a \(R\) jsou skalární funkce. Jiný běžný zápis je též \[\vec F=P(x,y,z)\vec i + Q(x,y,z)\vec j + R(x,y,z)\vec k\] nebo \[\vec F=P(x,y,z)\vec e_1 + Q(x,y,z)\vec e_2+ R(x,y,z)\vec e_3.\]
Limita a spojitost jsou ve světě funkcí více proměnných mnohem obtížnější pojmy než je tomu ve světě funkcí více proměnných. Proto se u spojitosti omezíme pouze na vyslovení definice a konstatování, že pokud máme funkci zadanou konečným analytickým předpisem, je tato funkce spojitá všude, kde je definovaná.
Definice (spojitost skalární funkce).
Nechť \(f:\mathbb{R}^n\to \mathbb{R}\) je funkce \(n\) proměnných definovaná v nějakém okolí bodu \(A\in\mathbb{R}^n\). Řekneme, že funkce \(f\) je v bodě \(A\) spojitá, jestliže pro každé okolí \(O(f(A))\) bodu \(f(A)\) existuje okolí \(\overline O(A)\) bodu \(A\) takové, že obrazy všech bodů z tohoto okolí bodu \(A\) leží v okolí bodu \(O(f(A))\), tj. pro všechna \(X\in \overline O(A)\) platí \(f(X)\in O(f(A))\).
Spojitost vektorové funkce je převedena na spojitost jednotlivých komponent.
Definice (spojitost vektorové funkce).
Nechť \(f:\mathbb{R}^n\to \mathbb{R}^m\) je vektorová funkce \(n\) proměnných definovaná v nějakém okolí bodu \(A\in\mathbb{R}^n\). Řekneme, že funkce \(f\) je v bodě \(A\) spojitá, jestliže je v tomto bodě spojitá každá její komponenta.
Obecně posoudit spojitost není lehké. V naprosté většině prakticky zajímavých případů však pracujeme jenom s jistou třídou funkcí, představenou v následující definici.
Definice (elementární funkce).
Všechny mnohočleny, goniometrické, cyklometrické, exponenciální a logaritmické funkce a obecná mocnina se nazývají základní elementární funkce Všechny funkce, které ze základních elementárních funkcí získáme konečným počtem operací sčítání, odečítání, násobení, dělení a skládání těchto funkcí navzájem se nazývají elementární funkce.
Jakmile se pohybujeme ve světě elementárních funkcí, je posouzení spojitosti snadné, jak ukazuje následující věta.
Věta (spojitost elementárních funkcí).
Všechny elementární funkce jsou spojité v každém vnitřním bodě svého definičního oboru.

Ani přesný vzorec pro vypočítaná data nás nezachrání, pokud je ve vstupních datech nejistota. Pomocí parciálních derivací dokážeme analyzovat, jak moc se výsledek rozmlží vlivem dat zatížených chybou. Zdroj: pixabay.com

Pocitová teplota v zimě závisí na skutečné teplotě a na síle větru. Pomocí parciálních derivací dokážeme analyzovat, co se bude s pocitovou teplotou dít při změnách vnějších podmínek. Zdroj: pixabay.com
Kanadský empirický vzorec pro pocitovou teplotu v zimě (wind-chill factor) je \[W(T,v) = 13.12+0.6215 T-11.37 v^{0.16}+0.3965 T v^{0.16},\] kde \(T\) je teplota (ve stupních Celsia) a \(v\) je rychlost větru (v km/hod). Teplota byla změřena \(-11.0\,{}^\circ\!\text{C}\) s chybou \(0.2\,{}^\circ\!\text{C}\) a rychlost \(26 \,\text{km/hod}\) s chybou \(5\,\text{km/hod}\). S využitím zákona šíření chyb určíme, jaký vliv mají nepřesnosti v měření na nepřesnost vypočítané veličiny.
Dosazením do vzorce dostáváme \(W(-11,26)=-20.212\,{}^\circ\!\text{C}\). Derivováním dostáváme \[\begin{aligned}\frac{\partial W}{\partial T}(T,v)&=0.6215+0.3965 v^{0.16},\\ \frac{\partial W}{\partial v}(T,v)&=-11.37\times 0.16 v^{-0.84}+0.3965 \times 0.16 Tv^{-0.84} \end{aligned} \] a po dosazení \[\begin{aligned}\frac{\partial W}{\partial T}(-11,26)&=1.289,\\ \frac{\partial W}{\partial v}(-11,26)&=-0.163 \,{}^\circ\!\text{C}\, \text{hod}/\mathrm{km}. \end{aligned} \] Za dané teploty a rychlosti větru způsobí nárůst teploty o jeden stupeň nárůst pocitové teploty přibližně o \(1.3\) stupně. Podobně, zesílení větru o jeden kilometr za hodinu způsobí snížení pocitové teploty přibližně o \(0.16\) stupně. Ze zákona šíření chyb dostáváme pro chybu pocitové teploty (dosazováno bez jednotek) \[\Delta W=\sqrt{\left(1.289\times 0.2\right)^2+\left(-0.163\times 5\right)^2}=0.85\,{}^\circ\!\text{C}.\] Pocitová teplota je tedy \(W=-20.2\,{}^\circ\!\text{C}\pm 0.9\,{}^\circ\!\text{C}\).

Při proudění tekutin nesledujeme jednotlivé molekuly, ale vektor rychlosti. Díky tomu můžeme stejným aparátem sledovat tok tekutiny, tok tepla nebo tok jiné veličiny. Zdroj: pixabay.com
Parciální derivace se vyskytují ve většině důležitých rovnic popisujících fyzikální svět okolo nás.
Parciální derivace umožňují sledovat závislost stavových veličin v závislosti na souřadnicích nebo čase, a to pro každou souřadnici samostatně. Nicméně souřadný systém je něco, co do popisu vnášíme uměle a proto by fyzikální proce neměl být na tomto souřadném systému závislý. Proto často spojujeme parciální derivace do složitějších výrazů -- diferenciálních operátorů. Zde teprve vynikne síla parciálních derivací.
Jedno z uplatnění je v mechanice kontinua při popisu proudění tekutin. Pomocí Newtonova zákona můžeme napsat pohybovou rovnici pro každou molekulu tekutiny a ze znalosti počáteční rychlosti a polohy všech molekul zjistit, jak bude vypadat pohyb molekul v libovolném čase. V praxi však nedokážeme ani přesně určit počet molekul, ne tak jejich počáteční polohu a rychlost. Jedním z přístupů odstraňujících tyto problémy je statistický přístup používaný ve statistické fyzice. Jiný přístup je, že nesledujeme pohyb jednotlivých molekul, ale v jednotlivých místech prostoru sledujeme důležité charakteristiky, jako například rychlost proudění nebo tlak v kapalině. To je přesně úloha pro diferenciální operátory sestavené z parciálních derivací.
Výhodou použití univerzálního nástroje parciálních derivací je, že získáme podobné rovnice pro studium řady rozdílných problémů. Při popisu proudění vycházíme ze zákona zachování: přírůstek proudící veličiny v uvažovaném místě tělesa je dán součtem vydatnosti všech zdrojů v tomto místě sníženém o množství veličiny, které vyteče přes hranice. Přitom spotřebiče uvažujeme jako zdroje se zápornou vydatností a tok dovnitř jako záporný tok. Na fyzikálním charakteru proudící veličiny nezáleží. Podobnými rovnicemi proto popisujeme proudění vody v potrubí (proudění homogenním prostředím, které neklade odpor), proudění vody ve dřevě (tj. proudění ortotropním materiálem), proudění vody nebo ropy v půdě (proudění anizotropním materiálem), proudění tepla v tepelně vodivém prostředí (proudění veličiny, která není spojena přímo s látkou) nebo například difuzi.

U teplokrevných živočichů vystavených chladu vzniká velký gradient teploty. Pro snížení tohoto gradientu a lepší ochranu před mrazem je výhodné mít silnou vrstvu chlupů. S rozdílem teplot teplokrevný živočich nic dělat nemůže, proto alespoň zvýší vzdálenost, podél které teplota klesá. Například ptáci se v zimě umí proměnit v načepýřené koule. Další výhodou je tlustá tuková tkáň.Zdroj: pixabay.com
V homogenním tíhovém poli s osou \(z\) svisle nahoru je gravitační potenciál (potenciální energie tělesa o jednotkové hmotnosti) dán vztahem \(\phi(x,y,z)=gz\) a gradient je konstantní vektor \(\nabla \phi=(0,0,g)\). Proto je práce přímo úměrná potenciálu a má smysl práci (změnu potenciální energie) považovat jenom za jiné vyjádření výškového rozdílu (změnu souřadnice \(z\)) Dokonce je to možné interpretovat jako změnu jednotek. Při proudění vody v půdě nebo v rostlinách hraje roli celá řada různých příspěvků k potenciální energii, jako gravitace, vnější tlak, osmóza, kapilarita. Pro pohodlnou práci někdy všechny tyto faktory přepočítáváme na odpovídající rozdíl výšek vodního sloupce, čímž je dána piezometrická hladina. Je to vlastně celková potenciální energie přepočtená na výšku vodního sloupce.
Většina proudění v přírodě je způsobena gradientem veličiny, která je hybatelnou silou tohoto proudění. Například vítr vznikne rozdílem v prostorovém rozložení tlaku (nenulovým gradientem). Často je intenzita proudění úměrná tomuto gradientu (Fickův zákon). Například hustota toku \(\vec j\) při difúzi vody ve dřevě je dána vztahem \[\vec j=-D\nabla c,\] kde \(c\) je koncentrace vody a \(D\) je difúzní konstanta.
Kanadský empirický vzorec pro pocitovou teplotu v zimě (wind-chill factor) je \[W(T,v) = 13.12+0.6215 T-11.37 v^{0.16}+0.3965 T v^{0.16},\] kde \(T\) je teplota (ve stupních Celsia) a \(v\) je rychlost větru (v km/hod). Teplota byla změřena \(-11.0\,{}^\circ\!\text{C}\) s chybou \(0.2\,{}^\circ\!\text{C}\) a rychlost \(26 \,\text{km/hod}\) s chybou \(5\,\text{km/hod}\).

Pocitová teplota v zimě závisí na skutečné teplotě a na síle větru. U zákona šíření chyb jsme vypočítali, jak se nejistota ve vstupních datech projeví ve výsledné veličině. Nyní vypočteme jednoduchý orientační vzorec pro pocitovou teplotu, jednodušší než výchozí přesný vztah, ale použitelný jenom pro limitovaný rozsah teplot a větru. Druhé dva členy jsou vlastně oprava k referenční hodnotě vyvolaná změnou vstupních veličin. Zdroj: pixabay.com
Na předchozích slidech jsme vypočítali \[\begin{aligned}W(-11,26)&=-20.212\,{}^\circ\!\text{C}\\\frac{\partial W}{\partial T}(-11,26)&=1.289,\\ \frac{\partial W}{\partial v}(-11,26)&=-0.163 \,{}^\circ\!\text{C}\, \text{hod}/\mathrm{km}. \end{aligned} \]
Přibližný vzorec pro pocitovou teplotu platný pro teploty blízké \(-11.0\,{}^\circ\!\text{C}\) a rychlosti větru blízké \(26 \,\text{km/hod}\) je \[W\approx -20.12 +1.289 (T+11) -0.163(v-26).\]
Poznámka (konstitutivní zákony).
V aplikacích často formulujeme pomocí gradientu a toku vektorového pole konstitutivní zákony. To jsou zákony nebo vztahy mezi fyzikálními veličinami specifickými pro danou látku nebo materiál a udávají odezvu tohoto materiálu na externí stimul. Viz. též Wikipedie.

Tok si snadno představíme mechanickým modelem. Například větru nebo vody. Zdroj: pixabay.com
Například vítr (tok molekul vzduchu) je vyvolán nerovnoměrným rozložením vzduchu (jeho hustoty a tím i tlaku) v prostoru a směřuje z míst s vyšším tlakem do míst s tlakem nižším. Větší rozdíl tlaků způsobí "větší vítr" a tím větší tok vzduchu. Toto platí i pro jiné proudění, jak ukážeme dále.
Nerovnoměrnost v prostorovém rozložení charakterizuje gradient. V ustáleném stavu je pro široké rozmezí fyzikálních problémů závislost intenzity toku na gradientu lineární. A protože nulovému gradientu (nulovému stimulu) odpovídá nulový tok (nulová odezva), bude tato lineární funkce přímou úměrností.
V dalším shrneme důležité praktické příklady, kdy je tok úměrný gradientu. Konstanta úměrnosti je obecně pouze konstantou pro daný problém a dané hodnoty parametrů. Může se měnit s velikostí studovaného objektu (například obsah průřezu geologické vrstvy, kterou proudí voda), s fyzikálními vlastnostmi proudící látky (např. viskozita nebo hustota tekutiny, stlačitelnost vzduchu), s fyzikálními vlastnostmi prostředí (např. velikost pórů v pórovitém prostředí nebo vlhkost dřeva). Proto je možné tyto zákony najít v různých tvarech, s různými členy a případnými přídavnými konstantami, které například odseparují vliv vlastností proudící látky a vliv vlastností prostředí. Vždy záleží na konkrétní situaci, zvyklostech v příslušném podoboru, nebo na přístupu autora. Není proto naší ambicí vést výklad dopodrobna, všímejme si jenom základních myšlenek.
Zákony uvedené níže byly často odvozeny v jednorozměrném případě. V moderní formulaci používáme obecný vektorový zápis, který zohledňuje i směr. Konstanta úměrnosti potom zprostředkovává vztah mezi dvěma vektory. Jedná se tedy z matematického pohledu o matici, která umožní nejenom změnit délku vektoru a jeho jednotku, ale i směr. Tato matice se navíc při změně báze transformuje speciálním způsobem, tak jako vektory. Takové objekty nazýváme tenzory. Níže budeme pojmem tenzor rozumět matici \(3\times 3\) nebo \(2\times 2\), podle kontextu. (Obecněji je možno považovat skalární veličiny a vektory za tenzory nižších řádů, toto my však dělat nebudeme.)
V roce 1855 německý lékař A. Fick objevil, že difuzní tok \(\vec J\) (množství látky které projde při difuzi jednotkovou plochou za jednotku času) je úměrný gradientu koncentrace \(c\) této látky. Matematicky vyjádřeno pomocí moderní terminologie to znamená, že platí \[\vec J=-D\nabla c. \] Veličina \(D\) se nazývá difuzní koeficient. Pokud má \(\vec J\) stejný směr jako \(\nabla c\), je \(D\) skalární veličina. Pokud směry nejsou stejné, je \(D\) tenzor. Z fyzikálních důvodů je tenzor \(D\) symetrický.
Difuzí se například dřevo zbavuje vlhkosti při vysoušení.

Vodárna Káraný infiltruje vodu do podzemí. Znalost, co se tam s vodou děje a kudy a jak teče je nezbytná. Základním zákonem pro popis tohoto děje je Darcyho zákon. Zdroj: nase-voda.cz, Nina Havlová
V letech 1855 a 1856 francouzský inženýr H. Darcy pokusy prokázal přímou úměru mezi rozdílem tlaků na koncích trubice naplněné porézní zeminou (jednalo se vlastně o rozdíl výšek pro šikmou trubici) a rychlost proudění vody touto trubicí. Tok (množství vody, která proteče jednotkovou plochou za jednotku času) je dán vztahem \[\vec q=-K\nabla p,\] kde \(p\) je tlak a \(K\) je koeficient vodivosti (někdy též koeficient filtrace), v obecném případě symetrický tenzor, v izotropním případě, kdy \(\vec q\) a \(\nabla p\) mají stejný směr, veličina skalární.
Někdy se tento zákon neformuluje pomocí gradientu tlaku, ale pomocí gradientu jiné veličiny, kterou zavádíme v hydrologii pro názorné studium efektů, souvisejících s prouděním vody. Nejčastěji se jedná o vodní potenciál a hydraulickou výšku či piezometrickou hladinu. Piezometrická hladina je veličina používaná k tomu, abychom do jednoho jednoduše modelovatelného faktoru (má rozměr stejný jako délka) započítali všechny veličiny mající vliv na proudění podzemní vody, od rozdílu nadmořských výšek, přes kapilární a osmotické jevy až po vnější síly vyvolané tlakem geologických vrstev a jiné. Jedná se vlastně o celkovou energii vody s tím, že některé části považujeme za zanedbatelné. Například často neuvažujeme kinetickou energii nebo osmózu a kapilární jevy.
Fourierův zákon se týká vedení tepla a vyjadřuje, že vektor hustoty tepelného toku \(\vec q\) je úměrný gradientu teploty \(\nabla T\) a má opačný směr, tj. \[\vec q=-D\nabla T.\] Je-li materiál anizotropní, což je nejobecnější případ, je veličina \(D\) symetrickým tenzorem. Je-li materiál izotropní, je \(k\) skalární veličinou, případně skalární veličina násobená jednotkovou maticí, pokud potřebujeme zachovat její maticový charakter.
Tok tepla je vyvolaný nerovnoměrným rozložením teploty. Difuze chemické látky je vyvolána nerovnoměrným rozložením koncentrace této látky. Většinou je hybatelem procesu nerovnoměrnost v rozložení látky, která se tímto procesem transportuje. Nemusí to však být vždy. Příkladem je termodifuze, což je pohyb prvků vyvolaný nerovnoměrným rozložením teploty. Například při difúzi vody ve dřevě s nerovnoměrným rozložením teploty je tok dán vztahem \[\vec J=-D\nabla c - sD\nabla T, \] kde \(s\) je koeficient termodifuze. Na rozdíl od předchozích zákonů, u Sortetova efektu dochází k transportu nejenom ve směru maximálního poklesu (záporného gradientu) teploty, ale někdy i ve směru gradientu teploty. Viz Wikipedia a heslo Thermophoresis.
Materiálová odezva na vnější podnět nemusí mít stejný směr jako podnět, například voda při vsakování do půdy nemusí tést přesně ve směru gravitační síly, ale směr může být odkloněn do směrů s větší hydraulickou vodivostí. Lineární vztah svazující dva vektory je možné zapsat pomocí maticového násobení, proto jsou konstanty v konstitučních zákonech v obecném případě matice (tenzory) Uvažujme vztah mezi gradientem a tokem ve tvaru \[\vec j=-K\nabla \varphi,\] kde \(K\) je symetrický tenzor. Gradient má ve trorozměrném případě vyjádření \[\nabla \varphi =\left(\frac{\partial \varphi}{\partial x},\frac{\partial \varphi}{\partial y},\frac{\partial \varphi}{\partial z}\right)^T\] a ve 2D \[\nabla \varphi =\left(\frac{\partial \varphi}{\partial x},\frac{\partial \varphi}{\partial y}\right)^T.\]
Veličina \(K\) je matice \[K= \begin{pmatrix} k_{11}& k_{12} & k_{13}\\ k_{21}& k_{22} & k_{23}\\ k_{31}& k_{32} & k_{33} \end{pmatrix} \] jejíž komponenty splňují \(k_{ij}=k_{ji}\). Často jsou všechny veličiny kladné a prvky v hlavní diagonále jsou dominantní.
Komponenty vektoru \(\vec j=(j_x, j_y, j_z)\) jsou \[ \begin{aligned} j_x&=-k_{11}\frac{\partial \varphi}{\partial x}-k_{12}\frac{\partial \varphi}{\partial y}-k_{13}\frac{\partial \varphi}{\partial z},\\ j_y&=-k_{21}\frac{\partial \varphi}{\partial x}-k_{22}\frac{\partial \varphi}{\partial y}-k_{23}\frac{\partial \varphi}{\partial z},\\ j_z&=-k_{31}\frac{\partial \varphi}{\partial x}-k_{32}\frac{\partial \varphi}{\partial y}-k_{33}\frac{\partial \varphi}{\partial z}, \end{aligned} \] což zjistíme prostým maticovým násobením. Prostor pro další úpravu není.

Ortotropní materiál je typicky materiál z jednotlivých vrstev. Typicky dřevo, půda z různých vrstev, lepenka. Zdroj: pixabay.com
V obecném případě je zpravidla možné transformovat soustavu souřadnic tak, aby tenzor \(K\) byl diagonální. Pro praktické výpočty se toto však často nevyplatí. Pokud však je studovaný problém ortotropní, má charakteristické směry (přesněji, má tři roviny symetrie materiálových vlastností), je možné zvolit souřadnice v souladu s těmito směry a matice \(K\) je diagonální.
\[K= \begin{pmatrix} k_{11}& 0 & 0\\ 0& k_{22} & 0\\ 0& 0 & k_{33} \end{pmatrix} \]
Komponenty vektoru \(\vec j\) jsou \[ \begin{aligned} j_x&=-k_{11}\frac{\partial \varphi}{\partial x},\\ j_y&=-k_{22}\frac{\partial \varphi}{\partial y},\\ j_z&=-k_{33}\frac{\partial \varphi}{\partial z}. \end{aligned} \]
S diagonální maticí se pracuje velmi dobře, protože má v hlavní diagonále vlastní čísla. Tato vlastní čísla jsou fyzikální charakteristikou úlohy. Například největší vlastní číslo a odpovídající vlastní směr charakterizují směr, ve kterém je odezva materiálu na vnější podnět maximální a vlastní číslo udává velikost této reakce. Tyto fyzikální charakteristiky nemohou být závislé na volbě souřadné soustavy, ve které úlohu popisujeme. Co se mění s volbou souřadné soustavy jsou pouze souřadnice vlastního vektoru. Vlastní čísla jsou však skalární a proto jsou invariantní při otočení soustavy souřadnic. Pokud bychom neměli možnost zvolit soustavu souřadnic tak, aby matice byla diagonální, máme alespoň jistotu, že vlastní čísla zůstanou stejná.
Stejné jako ve 3D, pouze chybí třetí rovnice.
Stejné jako ortotropní případ, ale navíc platí \(k_{11}=k_{22}=k_{33}=k.\) Potom \(\vec j=-k\nabla \varphi\), kde \(k\) je konstanta a vektory toku a gradientu mají opačný směr.
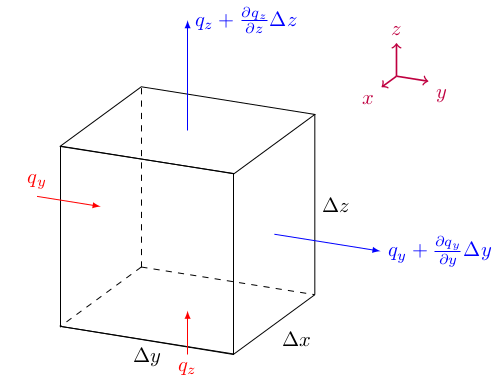
Divergence a tok pole \(\vec q=(0,q_y, q_z)\) krychlí. Tok je zobrazen vždy ve středu stěny. Červené vektory vstupují do krychle a příslušné toky se počítají záporně. Modré vystupují ven a počítají se kladně. V tomto případě je celková bilance kladná, z objemu více vyteče, než vteče dovnitř. Divergence je kladná. Pokud v krychli množství veličiny neubývá, musí tam být zdroj této veličiny.
V odvození matematického popisu proudění tepla (sušení dřeva), vody (sušení dřeva, tok podpovrchové vody), vzduchu (rovnice pro předpověď počasí) nebo dalších fyzikálních objektů či veličin hrají zásadní roli zákony zachování.
Při formulování zákonu zachování pro proudící veličinu musíme sledovat tok této veličiny, popsaný pomocí vhodného vektorového pole, ze zvoleného místa. Vyjádříme bilanci, o kolik je větší tok vektorového pole z daného místa ven ve srovnání s tokem tohoto pole dovnitř (viz krychlička na obrázku). Protože záleží na objemu, ve kterém tok sledujeme, je vztáhneme tento tok na jednotku objemu.
Fyzikálně tok ven uvažujeme jako kladný a tok dovnitř jako záporný. Velikost toku rovinnou plochou určíme jako součin vektorového pole v tomto místě a obsahu plochy. Celkový tok \(\vec q=(0,q_y,q_z)\) do krychle na obrázku je součtem toků levou boční stěnou a dolní stěnou, tj. \[Q_{in}=-q _y\Delta x \Delta z - q _z\Delta x \Delta y.\] Podobně tok ven z krychle je \[Q_{out}=\left(q_z+\frac {\partial q_z}{\partial z}\Delta z\right)\Delta x\Delta y + \left(q_y+\frac {\partial q_y}{\partial y}\Delta y\right)\Delta x\Delta z\] a celková bilance je \[Q_{in}+Q_{out}= \left(\frac {\partial q_y}{\partial y}+\frac {\partial q_z}{\partial z}\right)\Delta x\Delta y\Delta z. \] V případě proudění i v ose \(x\) bude přítomen ještě další analogický člen charakterizující tuto dodatečnou položku. Těmito úvahami je motivována následující definice a věta. (Definice je maličko nepřesná, protože nemáme nástroje pro pečlivější formulaci.)
Definice (divergence).
Divergence vektorového pole \(\vec F\) v daném bodě je převis toku vektorového pole z tohoto místa nad tokem do tohoto místa. Tento tok se počítá přes hranici infinitezimálně malého referenčního tělesa a je vztažený na jednotku objemu. Divergenci vektorového pole \(\vec F\) označujeme \(\mathop{\mathrm{div}}\vec F\) nebo \(\nabla \cdot \vec F\).
Věta (výpočet divergence).
Pro vektorovou funkci \[\vec F=(P,Q,R)=P\vec i + Q\vec j + R\vec k,\] kde \(P\), \(Q\) a \(R\) jsou funkce tří proměnných \(x\), \(y\) a \(z\) vypočteme divergenci vztahem \[\mathop{\mathrm{div}}\vec F=\nabla\cdot\vec F=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}.\] Pro vektorovou funkci dvou proměnných vypočteme divergenci analogicky, pouze chybí třetí člen.
Pokud při ustáleném proudění je v některém místě kladná divergence, znamená to, že v tomto místě musí být zdroj této veličiny. Proto se vektorové pole, jehož divergence je rovna nule, se nazývá nezřídlové pole.
Ze střední školy z fyziky umíme modelovat vektorové pole pomocí siločar. Siločáry nezřídlového pole nikde nezačínají ani nekončí a jsou to uzavřené křivky. Například stacionární magnetické pole je nezřídlové. Absence zdrojů magnetického pole se projevuje tak, že rozříznutím tyčového magnetu vzniknou dva menší plnohodnotné magnety. Nevznikne samostatný jižní pól a samostatný severní pól magnetu. To je rozdíl oproti poli elektrickému, kdy rozdělením tyče s opačně nabitými konci vznikne jedna kladně nabitá a jedna záporně nabitá tyč poloviční délky.

Rovnice kontinuity je vlastně bilance zisků a ztrát pro danou stavovou veličinu v libovolném bodě. Zdroj: pixabay.com
Zformulujeme zákon zachování pro zcela obecný případ zachovávající se veličiny. Díky obecnému přístupu jsou rozsáhlé aplikace, ale k nim je nutné dodat další informace o studovaném problému (z biologie, geologie, fyziky, ...).
Předpokládejme, že tok vektorového pole přenáší nějakou stavovou veličinu (veličinu, která charakterizuje stav látky nebo tělesa). Množství této veličiny v jednotkovém objemu tělesa označíme \(\rho\). Budeme uvažovat obecný nestacionární stav, kdy se \(\rho\) může měnit s časem.
Poznámka (zákon zachování).
Rovnice kontinuity je matematické vyjádření zákona zachování. Udává, že pro libovolnou malou reprezentativní část tělesa je rychlost změny množství stavové veličiny dána celkovou vydatností zdrojů v této části snížené o tok z této části tělesa ven.
Pomocí divergence můžeme zákon zachování vyjádřit kvantitativně. Podle výše uvedeného platí \[\frac{\partial \rho}{\partial t} =\sigma-\mathop{\mathrm{div}} \vec j \] neboli \[\frac{\partial \rho}{\partial t}+\mathop{\mathrm{div}}\vec j = \sigma.\] Tato rovnice se nazývá rovnice kontinuity a díky své obecnosti popisuje širokou škálu problémů týkajících se živé i neživé přírody. Při praktickém použití většinou preferujeme názornou interpretaci jednotlivých veličin a proto se v rovnici mohou objevit další konstanty úměrnosti, které umožní sladit jednotky a fyzikální interpretaci členů. Někdy se naopak snažíme konstanty co nejvíce redukovat metodami transformace které si představíme v přednášce o diferenciálních rovnicích. Proto volíme vhodné násobky veličin vystupujících v matematické formulaci tak, aby se co nejvíce konstant eliminovalo, případně shluklo do jediné veličiny. Zkušenosti ukazují, že je vhodné volit veličiny bezrozměrné. Například v publikaci P. Horáček, Fyzikální a mechanické vlastnosti dřeva I je zavedena bezrozměrná vlhkost, bezrozměrný čas a bezrozměrná vzdálenost na straně 61 pro rovnici popisující difuzi a charakteristická délka, Biotovo číslo (bezrozměrná tepelná vodivost) a bezrozměrná teplota, bezrozměrný čas a bezrozměrná vzdálenost pro rovnici popisující vedení tepla na stranách 88 a 89.
V této rovnici není zahrnut případ, kdy se veličina přenáší ještě i prouděním hmotného prostředí (konvekce).

Rovnice vedení tepla se využívá při modelování ohřevu nebo ochlazování. Zdroj: pixabay.com.
Důležitým speciálním případem rovnice kontinuity je vedení tepla, kdy dochází k přenosu energie a rovnice kontinuity vyjadřuje, že energie nemizí ani se netvoří. Proto má rovnice vedení tepla zpravidla nulový člen vyjadřující vydatnost zdrojů a tvar
\[\rho c\frac{\partial T}{\partial t}+\mathop{\mathrm{div}}\vec j = 0,\tag{1}\] kde \(T\) je teplota, \(\vec j\) tok tepla. Konstanty \(\rho\) a \(c\) jsou hustota a měrná tepelná kapacita a slouží k přepočtení množství dodaného tepla na lépe měřitelnou veličinu, na změnu teploty.
Pokud k tomuto tvaru rovnice kontinuity přidáme Fourierův zákon a divergenci převedeme na druhou stranu rovnice, získáme \[\rho c\frac{\partial T}{\partial t}=\mathop{\mathrm{div}} (D\nabla T).\] To je zobecnění rovnice vedení tepla v jedné dimenzi, kterou jsme odvodili primitivními prostředky (jenom pomocí parciálních derivací, bez gradientu a divergence) v úvodní přednášce.
V některých případech nemusí být člen charakterizující zdroje nulový. Teplo může vznikat například při tření nebo při průchodu elektrického proudu transformací z jiného druhu energie.
Ze střední školy známe makroskopickou formu rovnice (1) \[mc\Delta T=Q.\] Ta je zformulována pro těleso jako celek a \(Q\) se uvažuje v opačném smyslu než v rovnici kontinuity (teplo je kladné, pokud jej dodáváme).
V literatuře věnované problematice dřeva se rovnice vedení tepla ve dřevě označuje jako Druhý Fourierův zákon (P. Horáček, Fyzikální a mechanické vlastnosti dřeva I, str. 88).

Rovnice mechaniky kontinua dokáží popsat i děje, které se odehrávají v tekutinách tekoucích jinak, než voda nebo ideální tekutina. Běžným příkladem je med, technicky významným například beton. Kromě rovnice kontinuity je nutné dodat ještě další fyzikální vztahy. Zdroj: pixabay.com.
V mechanice kontinua podobně jako u vedení tepla neuvažujeme zdroje. Rovnice kontinuity popisující proudění dané rychlostí \(\vec u\) má poté tvar \[\frac{\partial \rho}{\partial t} + \mathop{\mathrm{div}} (\rho \vec {u}) = 0,\] kde \(\rho\) je hustota. Tato rovnice napsána pro vzduch je jednou z rovnic používaných při modelování vývoje počasí
Pro nestlačitelnou tekutinu je hustota dále konstantní a odsud dostáváme \[\mathop{\mathrm{div}} \vec u =0.\] Důsledkem této rovnice je zvýšení rychlosti molekul pohybující se nestlačitelné tekutiny při proudění místem s menším průřezem.
Středoškolský makroskopický tvar jednorozměrné rovnice kontinuity pro proudění nestlačitelné tekutiny je \[S u = \mathrm{konst}.\]

Proudění vody ve dřevě nás zajímá zejména u sušení. Ale podobně můžeme modelovat i vlhnutí. Zdroj: Wikipedia (Hbkrako).
Jedná se o rovnici kontiunity pro koncentraci vody \(c\). Voda ve dřevě nevzniká ani nezaniká, jenom se transportuje mimo dřevo. Proto v rovnici nebudou zdroje. Příslušným konstitutivním zákonem je Fickův zákon. Rovnice popisující tento proces má tvar \[\frac{\partial c}{\partial t}=\mathrm{\mathop{div}}(D\nabla c)\tag{*}\] anebo (po započtení Soretova efektu) \[\frac{\partial c}{\partial t}=\mathrm{\mathop{div}}(D\nabla c+sD\nabla T).\] Ve druhém případě musíme tuto rovnici uvažovat společně s rovnicí vedení tepla a mít tedy úlohu na soustavu dvou rovnic pro dvě modelovaná pole.
V případě dřeva volíme pokud možno souřadné osy souhlasně s anatomickými směry dřeva a matice \(D\) je poté diagonální. Proto se (*) redukuje na \[ \frac{\partial c}{\partial t}=\frac{\partial }{\partial x}\left(D_x\frac{\partial c}{\partial x}\right)+\frac{\partial }{\partial y}\left(D_y\frac{\partial c}{\partial y}\right)+\frac{\partial }{\partial z}\left(D_z\frac{\partial c}{\partial z}\right) \] Považujeme-li složky matice \(D\) za konstanty (nemusely by být, protože materiál buď nemusí být homogenní, nmebo může mít nelineární odezvu a \(D\) m,ůže záviset na \(c\)), je možné psát rovnici ve tvaru \[ \frac{\partial c}{\partial t}=D_x\frac{\partial^2 c}{\partial x^2}+D_y\frac{\partial^2 c}{\partial y^2}+D_z\frac{\partial^2 c}{\partial z^2}, \tag{**} \] protože derivace konstantního násobku je násobek derivace.
V literatuře věnované problematice dřeva se rovnice difuze použitá na modelování vlhkosti ve dřevě označuje jako Druhý Fickův zákon (A. Požgaj a kol., Štruktúra a vlastnosti dreva, str. 202, P. Horáček, Fyzikální a mechanické vlastnosti dřeva I, str. 60).
V praxi je dřevo často s jistou přesností homogenní, ale difuzní koeficient dřeva závisí na vlhkosti, tedy vztah mezi gradientem vlhkosti a difuzním tokem není lineární. Přesto i v tomto případě používáme Fickův zákon, ovšem složky difuzního koeficientu nepovažujeme za konstanty, jsou závislé na \(c\) a jejím prostřednictvím i na \(x\). Ani takovém případě si úpravu na rovnici (**) nemůžeme dovolit.

Modelování pohybu podzemní vody je důležité pro nastavení správného režimu hospodaření s vodou, nebo pro účinnou ochranu zdrojů vody před kontaminací. V místě kde hladina podzemní vody sahá k povrchu je studánka. Na obrázku Dykova studánka na ŠLP MENDELU v Brně. Zdroj: turistika.cz.
Podzemní vodou se rozumí voda přítomná pod zemským povrchem, která teče porézním prostředím tvořeným propustnými horninami a geologickými vrstvami nad nepropustnou vrstvou (volná hladina) nebo mezi dvěma nepropustnými vrstvami (napjatá hladina).
Stavovou veličinou při proudění podzemní vody s volnou hladinou je piezometrická výška \(h\). (Pro jednoduchost si představme hladinu podzemní vody.)
Obecný tvar rovnice kontinuity pro podzemní vodu, ve kterém uvažujeme nestlačitelnou kapalinu, nestacionární stav a zdroje či spotřebiče (například prosak do jiných geologických vrstev, mimo vodní kolektor) má tvar \[S\frac{\partial h}{\partial t} +\mathop{\mathrm{div}} \vec q=P,\] kde \(\vec q\) je tok, \(P\) je celkový objem ze zdrojů, \(h\) je piezometrická výška a \(S\) je měrná objemová zásobnost (kolik vody se uvolní z jednotkového množství půdy při změně piezometrické výšky o jednotku). Tato rovnice vyjadřuje, že rozdíl mezi množstvím vody, které z místa vyteče a množstvím, které do místa vteče, je dán vydatností zdroje v tomto místě a tím, kolik vody v tomto místě ubude díky snížení piezometrické hladiny (u volné hladiny jde zejména o snížení hladiny podzemní vody, u napjaté hladiny souvisí zejména se změnou pórovitosti při změně tlaku).
S Darcyho zákonem vyjádřeným pomocí piezometrické výšky, tj. \[\vec q=-k\nabla h,\] a bez dodatečných zdrojů (\(P=0\)) obdržíme \[\mathop{\mathrm{div}} \left(k\nabla h\right)=S\frac{\partial h}{\partial t}.\] Často je vertikální proudění zanedbatelné a úloha není trojrozměrná, ale ve skutečnosti dvourozměrná a pro třetí souřadnici klademe \[\frac{\partial h}{\partial z}=0\] (Dupuitův předpoklad). Pokud je možnost zvolit soustavu tak, že geometrické vlastnosti jsou v souladu s fyzikálními (jedna osa je ve směru největší a druhá ve směru nejmenší vodivosti), je tenzor \(k\) diagonální a rovnice se redukuje na \[\frac{\partial }{\partial x} \left(k_x \frac{\partial h}{\partial x}\right) + \frac{\partial }{\partial y} \left(k_y \frac{\partial h}{\partial y}\right) = S\frac{\partial h}{\partial t}. \] Pokud jsou fyzikální vlastnosti stejné ve všech bodech uvažované oblasti, jsou \(k_x\) a \(k_y\) konstanty a úloha se dále redukuje na \[k_x \frac{\partial^2 h}{\partial x^2} + k_y \frac{\partial^2 h}{\partial y^2} = S\frac{\partial h}{\partial t}. \]
Pro ustálené proudění (\(h\) se nemění v čase) v těchto rovnicích platí \[\frac{\partial h}{\partial t}=0.\] Je-li navíc \(k_x=k_y\) (izotropie, stejné vlastnosti ve obou hlavních směrech a tedy i ve všech směrech ostatních), redukuje se tato rovnice popisující proudění podzemní vody na rovnici \[\frac{\partial ^2 h}{\partial x^2}+\frac{\partial^2 h}{\partial y^2}=0.\]