
Derivace teploty je rychlost změny teploty. Zdroj: pixabay.com
Pokud funkce \(f(x)\) popisuje veličinu, která nás zajímá, potom \[f(x+h)-f(x)\] je změna této veličiny na intervalu \([x+h,x]\) a \[\frac{f(x+h)-f(x)}{h}\] je průměrná změna této veličiny, vztažená na jednotku veličiny \(x\) (průměrná rychlost změny \(f\) při změnách \(x\)). Tato veličina je závislá na \(h\), na délce intervalu. Limitním přechodem můžeme učinit \(h\) rovno nule, což nás vymaní ze závislosti na \(h\) a z průměrné rychlosti dostáváme rychlost okamžitou. To je obsahem definice derivace, jak ji známe z předchozích kurzů matematiky (většinou úvodní kurz matematiky na VŠ, někdy poslední ročník SŠ). \[f'(x)=\frac{\mathrm{d}f}{\mathrm{d}x}=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}\]
Derivace je okamžitá rychlost změny.

Derivace teploty je rychlost změny teploty. Zdroj: pixabay.com
Hrnek kávy v místnosti o teplotě \(20^\circ\mathrm{C}\) se ochladí z teploty \(95^\circ\mathrm{C}\) na \(25^\circ\mathrm{C}\) například za \(40\) minut. To znamená, že nápoj chládne rychlostí \[\frac{25-95}{40} \,{}^\circ\mathrm{C}\, \mathrm{min}^{-1}=-1.75^\circ\mathrm{C}\, \mathrm{min}^{-1},\] tj. každou minutu se nápoj ochladí průměrně o necelé dva stupně Celsia. Toto však není příliš realistický model. Horký nápoj chládne rychleji, protože je tepelná výměna intenzivnější díky většímu rozdílu teploty nápoje a místnosti. Realističtějším modelem popisujícím závislost teploty na čase je funkce \[T(t)=20+75 e^{-0.0677t}.\] Derivace této funkce \[\frac {\mathrm dT}{\mathrm dt}=-75\cdot 0.0677 e^{-0.0677t}\] udává rychlost změny teploty v libovolném čase. Pro \(t=0\) a \(t=40\) dostáváme \[\frac {\mathrm dT}{\mathrm dt}(0)=-5.08 ^\circ\mathrm{C}\, \mathrm{min}^{-1},\qquad \frac {\mathrm dT}{\mathrm dt}(40)=-0.34 ^\circ\mathrm{C}\, \mathrm{min}^{-1}, \] tedy na počátku chládne rychlostí pět stupňů Celsia za minutu, na konci už jenom rychlostí necelého půl stupně za minutu.
Ze známé rychlosti změny veličiny je možné zrekonstruovat změnu této veličiny.

Pokud dírou ve dně vytéká voda ze sudu, rychlost je na počátku větší (u dna je při větší hloubce větší tlak) a snižuje se. Klasický přístup hledání celkové změny pomocí násobení rychlosti s délkou časového intervalu selhává vinou nekonstantní rychlosti. Zdroj: pixabay.com
V nádrži je metr vody a voda vytéká tak, že hladina klesá rychlostí \(20\mathrm{cm}\,\mathrm{h}^{-1}\). Touto rychlostí by voda vytekla za pět hodin. Protože však s objemem vody klesá tlak u dna, výtoková rychlost se snižuje. V případě nádrže se svislými stěnami by byl realistický model popisující závislost rychlosti snižování hladiny na čase \[\frac{\mathrm dh}{\mathrm dt}=(-0.2 + 0.02 t)\,\mathrm{m}\,\mathrm{hod}^{-1}.\] Za prvních pět hodin vyteče \[h(5)-h(0)=\int_0^5 \frac{\mathrm dh}{\mathrm dt} \,\mathrm dt=\int_0^5 (-0.2 + 0.02 t) \,\mathrm dt=\left[-0.2 t + 0.01 t^2\right]_0^5 = -0.75\,\mathrm m \] a voda tedy klesne o třičtvrtě metru. Po pěti hodinách nádrž ještě není prázdná, ale je v ní pořád čtvrtina vody. Ta bude vytékat ještě dalších pět hodin, protože \[h(10)-h(5)= \int_5^{10} (-0.2 + 0.02 t) \,\mathrm dt= -0.25\,\mathrm m \]
Derivace nejčastěji ve fyzikálních zákonech vystupuje jako rychlost změny v čase, často vyjádřená slovy "časová změna"
Newtonův zákon síly (pohyb hmotného tělesa na které působí vnější síla): Časová změna hybnosti je rovna výsledné působící síle. \[\frac{\mathrm d p}{\mathrm dt}=F\]

Newtonův pohybový zákon, založený na derivaci, umožňuje kvantifikovat účinky všech sil na pohyb. Na Zemi i ve vesmíru. Zdroj: pixabay.com
Tj. derivace hybnosti podle času je rovna výsledné síle. Hybnost je součinem hmotnosti a rychlosti \[p=mv\] a její derivace je pro tělesa s konstantní hmotností součinem hmotnosti a derivace rychlosti, tj. zrychlení. \[\frac{\mathrm d p}{\mathrm dt}=m \frac{\mathrm d v}{\mathrm dt} = m a \] Zrychlení je druhá derivace polohy. Nejčastěji proto tento zákon píšeme ve tvaru \[m\frac{\mathrm{d}^2 x}{\mathrm{d}t^2}=F.\]
Speciální případy dobře známé ze střední školy jsou zákon setrvačnosti (\(F\) nulová), rovnoměrně zrychlený pohyb (\(F\) nenulová konstantní) a kmitavý pohyb na pružině (\(F=-kx\)).
Faradayův zákon elmg. indukce (indukované napětí podél uzavřené smyčky v proměnném magnetickém poli): Hodnota indukovaného elektromotorického napětí je rovna záporně vzaté časové změně celkového magnetického toku, který prochází elektrickým obvodem.

Větší rychlost jízdního kola znamená větší derivaci magnetického toku podle času a větší svit žárovky. Zdroj: pixabay.com
\[\mathcal E = -\frac{\mathrm d\Psi}{\mathrm dt}\] Speciálním případem známým ze střední školy je přímý vodič pohybující se v homogenním magnetickém poli po rovnoběžných vodičích.

Derivace hraje roli při odvození podmínky pro vznik hydraulického skoku. Zdroj: Jonathan Ball, https://www.flickr.com/photos/jball359
Při přechodu bystřinného proudění v říční vzniká hydraulický skok. Při odvození podmínky vzniku tohoto skoku hraje důležitou roli derivace obsahu průřezu koryta podle výšky koryta. Tato veličina vyjadřuje, jak rychle se mění obsah průřezu s rostoucí hladinou. Po nakreslení obrázku s příčným řezem korytem je zřejmé, že tato derivace je rovna šířce koryta v místě hladiny. V praxi je toto možné spočítat pro speciální tvary koryta, proto jsou explicitní fyzikálně podložené vzorce pro vodní skok k dispozici jenom ve speciálních případech, jako například koryto obdélníkového tvaru.
Nerovnoměrnost rozložení teploty v tělese vede k vyrovnávání teplot přenosem tepla. Uvažujme teplotu \(T\) tyče jako funkci polohy \(x\) na tyči. Ke kvantitativnímu vyjádření vedení tepla je nutné vědět, jaký rozdíl teplot připadá na jednotku délky. V homogenním případě vydělíme teplotní rozdíl vzdáleností. V obecném případě rychlost s jakou se mění teplota podél tyče (gradient teploty) vyjadřujeme pomocí derivace \[\frac{\mathrm dT}{\mathrm dx}.\] Využívá se v posuzování izolačních vlastností a při sušení dřeva.
Často se setkáme s tím, že dvě nebo více veličin jsou svázány vzájemně jednoznačným vztahem a změna jedná veličiny vyvolává změnu veličiny další. Pomocí derivace a pomocí pravidla pro derivaci složené funkce je možné najít vztah mezi rychlostmi změn těchto veličin.

Pokud koule taje tak, že se poloměr zmenšuje konstantní rychlostí, objem se zmenšuje stále pomaleji a pomaleji. Zdroj: pixabay.com
Příklad: Ledová koule taje tak, že se poloměr zmenšuje rychlostí \(3\)cm/hod. Jak rychle se zmenšuje objem v okamžiku, kdy je poloměr \(10\)cm?
Řešení: Zadání vlastně říká následující: \(V=\frac 43 \pi r^3\), \(r=10\)cm, \(\frac {\mathrm{d}r}{\mathrm{d}t}=-3\)cm/hod, \(\frac {\mathrm{d}V}{\mathrm{d}t}=?\)
Derivací získáváme \[\frac {\mathrm{d}V}{\mathrm{d}t}= 4\pi r^2 \frac {\mathrm{d}r}{\mathrm{d}t}\] a po dosazení \[\frac {\mathrm{d}V}{\mathrm{d}t}= 4 \cdot \pi \cdot (10\mathrm{cm})^2\cdot (-3)\mathrm{cm}/\mathrm{hod}=-3800 \mathrm{cm}^3/\mathrm{hod}.\]
Objem koule se zmenšuje rychlostí 3800 krychlových centimetrů za hodinu. To je zdánlivě vysoké číslo vzhledem k objemu celé koule (4100 krychlových centimetrů), ale všimněme si, že rychle klesá s klesajícím poloměrem.
Je-li známa současná hodnota veličiny \(f\) a rychlost změny této veličiny, je možno budoucí nebo minulou hodnotu veličiny \(f\) odhadnout extrapolací za předpokladu, že rychlost změny bude resp. byla stále stejná.
\[f(x)\approx f(a)+f'(a)(x-a)\]
Toto je základní vztah pro lokální lineární aproximaci, pro nahrazení komplikovaných vztahů jejich lineárními přiblíženími.
Příkladem jsou vztahy pro umocňování a odmocňování čísel blízkých jedniččce \[(1\pm x)^n\approx 1\pm nx ,\quad \text{pro malé }x.\]
Dvě základní aplikace tohoto vztahu vedou na vzorce známé ze středoškolské fyziky: středoškolské vztahy pro energii pohybujícího se tělesa a pro potenciální energii pro malé výšky nad povrchem Země jsou aproximací přesných vztahů plynoucích z Einsteinovy teorie relativity a z Newtonovy gravitační teorie. Ač se jedná "jenom" o lineární aproximace, jsou dokonce mnohem použitelnější, protože výpočet kinetické energie pomocí univerzálně platného vzorce při malých rychlostech zhavaruje na zaokrouhlovacích chybách.
\[E=\frac{m_0c^2}{\sqrt{1-\frac {v^2}{c^2}}} =m_0 c^2 \left(1-\frac {v^2}{c^2}\right)^{-1/2} \approx m_0c^2+\frac 12 m_0v^2 \quad \text{pro $v$ mnohem menší než $c$}\]
\[V = -\kappa \frac{mM}{R+h} =-\kappa \frac{mM}{R}\left (1+\frac hR\right)^{-1} \approx -\kappa \frac{mM}{R} + \kappa \frac{mM}{R^2} h =E_0+m g h,\quad \text{kde $g=\kappa \frac{M}{R^2}$}\]

Některé úlohy je nutné řešit numericky. I v takovém případě je linearizace vhodným nástrojem pro zjednodušení problému. Zdroj: pixabay.com
Z lineární aproximace \[f(x)\approx f(a)+f'(a)(x-a)\] pro \(a=x_n\), \(x=x_{n+1}\), \(f(x_{n+1})=0\) dostáváme \[x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}.\] Tímto způsobem můžeme numericky hledat nulové body funkcí, což v sobě zahrnuje i řešení rovnic. Například pro rovnici \[x=\cos x\] a počáteční odhad \(x_0=1\) hledáme vlastně nulový bod funkce \(f(x)=x-\cos x\). Po dosazení \(f'(x)=1+\sin x\) získáváme iterační vzorec \[x_{n+1}=x_n-\frac{x_n-\cos x_n}{1+\sin x_n}\] a jednotlivé iterace s aproximací na 80 desetinných míst dávají postupně následující hodnoty.
0.75036386784024389303494230668217685324699306585535903096658315202443061372724844
0.73911289091136167036058529090489023400289283673565690732340797067262734474030949
0.73908513338528396976012512085680433288953312317018897963123060924114905347788420
0.73908513321516064166170262568502637232522326252964269151340253531790167136371866
0.73908513321516064165531208767387340401342077636703525840515904303894688001184009
0.73908513321516064165531208767387340401341175890075746496568063577328465488354759
0.73908513321516064165531208767387340401341175890075746496568063577328465488354759Vidíme, že proces neuvěřitelně rychle konverguje k řešení rovnice. Každým krokem se přibližně zdvojnásobí počet desetinných míst, která jsou správně.

Mnoho procesů se řídí zákony zachování. Pokud proudící látka může vznikat a zanikat nebo měnit hustotu, není situace tak jednoduchá, jak to známe z rovnice kontinuity ve středoškolské fyzice. Zdroj: pixabay.com
Derivace je vhodná ke studiu fyzikálních procesů na makroskopické úrovni těles. Takovým fyzikálním zákonům říkáme zákony v integrálním tvaru. Ty jsou často odvozeny ze zákonů zachování.
Pro vyjadřování procesů jako jsou rychlost změny teploty tělesa nebo množství tekutiny v daném objemu jsou vhodné (obyčejné) derivace.
Někdy však požadujeme detailnější informace o celém procesu, abychom měli přesnější popis a dokázali odhalit vliv všech relevantních parametrů. U tepelné výměny bychom například sledovali, jak se teplo předává z jednoho místa tělesa do druhého místa a jak prostupuje tělesem. Takový pohled je nutný například při studiu procesu, který není stacionární v čase. Při tomto pohledu již musíme znát teplotu nejen jako funkci času, ale i jako funkci prostorových souřadnic. Výsledkem tohoto přístupu je formulace zákonů v diferenciálním tvaru. Tento tvar říká, co se děje v konkrétním místě a dává lepší náhled na fyzikální podstatu. Proto tomuto přístupu často dáváme přednost a používáme jej jako výchozí bod pro studium a popis konkrétních situací. Musíme tedy pracovat s funkcemi více proměnných a studovat, jak se mění vzhledem k jednotlivým proměnným. To je přesně úkol pro diferenciální počet funkcí více proměnných a parciální derivace.
![Parciální derivace funkce f v bodě [2,-2] jsou derivace křivek vzniklých na řezech rovinami x=2 a y=-2.](parcialni_derivace_1.png)
Parciální derivace funkce \(f\) v bodě \([2,-2]\) jsou derivace křivek vzniklých na řezech rovinami \(x=2\) a \(y=-2\).

Energie potřebná pro překonání pevné vzdálenosti závisí na hmotnosti jedince a na rychlosti, kterou vyvíjí. Zdroj: pixabay.com
Energie \(E\) (v kcal), kterou spotřebuje ještěrka o hmotnosti \(m\) (v gramech) na překonání vzdálenosti jednoho kilometru rychlostí \(v\) (v kilometrech za hodinu) se dá odhadnout vzorcem \[E(m,v)=2.65 m^{0.66} + \frac{3.5 m^{0.75}}{v}.\] Přímým výpočtem je možné určit \[\frac{\partial E}{\partial v}=-\frac{3.5 m^{0.75}}{v^2}.\] Pro \(m=400\,\mathrm{g}\) a \(v=8\,\mathrm{km}\,\mathrm{h}^{-1}\) dostáváme \[\frac{\partial E}{\partial v}(400,8)=-4.9\,\mathrm{kcal}\,\mathrm{km}^{-1}\mathrm{h}.\] Zvýšení rychlosti o kilometr za hodinu vede ke snížení energetického výdeje ještěrky o \(4.9\,\mathrm{kcal}\). Podobně, platí \[\frac{\partial E}{\partial m}= {2.65}\times 0.66 {m^{-0.34}} + \frac{3.5\times 0.75 m^{-0.25}}{v}= \frac{1.749}{m^{0.34}} + \frac{2.625}{m^{0.25} v} \] a pro výše uvažované hodnoty dostáváme \[\frac{\partial E}{\partial m}(400,8)= 0.30\,\mathrm{kcal}\,\mathrm{g}^{-1}. \] Každý gram, který má ještěrka navíc oproti hmotnosti \(400\) gramů, zvedne energetický výdej přibližně o \(0.30\,\mathrm{kcal}\).
(Zpracováno podle Stewart: Biocalculus)

Brzdy v autě musí absorbovat kinetickou energii, která je lineární funkcí hmotnosti a kvadratickou funkcí rychlosti. Zdroj: pixabay.com
Brzdná dráha \(L\) (v metrech) auta o hmotnosti \(m\) (v kilogramech) brzdícího z rychlosti \(v\) (v kilometrech za hodinu) je dána vzorcem \[L=k\ m v^2, \] kde \(k= 3.45 \times 10 ^{-6}\,(\mathrm{m}\,\mathrm{hod}^2)/(\mathrm{kg}\,\mathrm{km}^2)\). Pro \(m=1100\,\mathrm{kg}\) a \(v=100\,\mathrm{km}/\mathrm{hod}\) je brzdná dráha \(37.95\,\mathrm{m}\).
Studujme vedení tepla v jednorozměrné tyči. (Zahrnuje i stěnu jako extrémně krátkou tyč extrémně velkého průřezu). Teplota je funkcí dvou proměnných, polohy a času.
Poznámka.
Potřebujeme fyzikální zákony řídící vedení tepla. Bez nich matematika model vedení tepla nemá jak naformulovat. Tyto zákony je potřeba matematice "dodat zvenku" a jsou následující.
- Rozdíl teplot má za následek pohyb tepla. Velikost toku tepla je úměrná teplotnímu rozdílu.
- Tok tepla je aditivní veličina, tj. celkový tok průřezem je součinem toku vztaženého na jednotku průřezu a obsahu průřezu.
- Teplota se zvyšuje dodáním tepla. Pro zvýšení teploty tělesa o hmotnosti \(m\) o hodnotu \(\Delta T\) je nutné dodat \[Q=mc\Delta T,\tag{*}\] kde \(c\) je měrná tepelná kapacita.
V dalším už nastupuje matematický popis a ve vhodných chvílích vždy použijeme výše uvedené fyzikální zákony. Mluvíme o teple, ale jako mechanický model si můžeme představit proudění tekutiny (pro jednoduchou představu) nebo proudění vlhkosti (pro odvození rovnice difuze namísto rovnice vedení tepla).
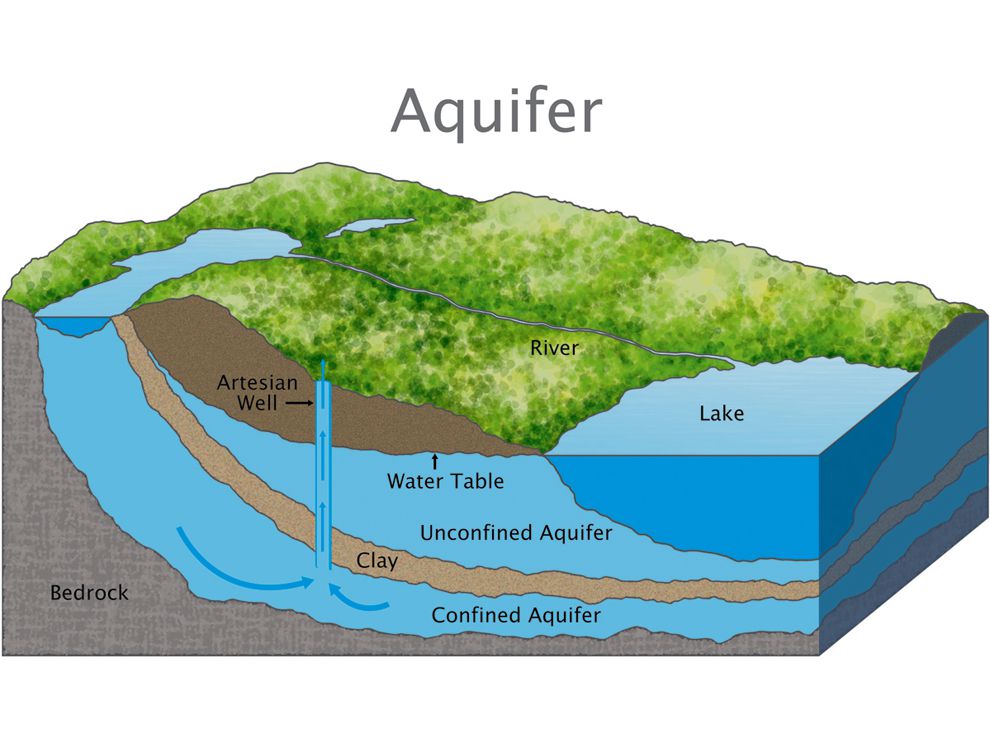
Z matematického hlediska je proudění podzemní vody popsáno stejnými rovnice jako proudění tepla. Zdroj: nationalgeographic.org
Odvodili jsme tvar rovnice vedení tepla v jednorozměrném prostředí. \[\frac{\partial}{\partial x}\left(k\frac{\partial T}{\partial x}\right)=\rho c\frac{\partial T}{\partial t}\]
V odvození vidíme, že tato rovnice je vlastně bilance toku tepla. Rozdíl o kolik se v daném místě snižuje tok tepla udává, kolik tepla se v daném místě spotřebovalo. Tato spotřeba tepla se projeví zvýšením teploty v daném bodě. Jedná se o speciální případ difuzní rovnice, se kterou se seznámíme později.
V odvození nebylo podstatné, že se jedná o vedení tepla. K rovnici podobného typu dospějeme, pokud matematicky formulujeme zákon zachování nějaké proudící veličiny. Proto rovnice tohoto typu (a jejich zobecnění do více dimenzí a pro případ existence zdrojů nebo spotřebičů) figurují v matematickém popisu difuze, sušení dřeva, vedení tepla nebo proudění tekutin, včetně proudění podzemní vody a proudění vzduchu.