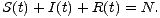
Pokusíme se sestrojit jednoduchý model procesů vzniku, šíření a odeznívání epidemií. Budeme se přitom zabývat tzv. modely bez vitální dynamiky, tj. budeme uvažovat, že celkový počet jedinců v populace se nemění v čase. K tomu budeme uvažovat, že choroba má krátké inkubační období a doba mezi nákazou jedince a jeho onemocněním je zanedbatelná. V tomto případě je možno populaci rozdělit do tří skupin.
Veličiny S,I,R jsou obecně funkcemi času. V libovolném časovém okamžiku t platí
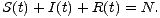
Uvedené požadavky je možno matematicky vyjádřit soustavou diferenciálních rovnic (Kermack-McKendrik(1927))
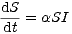 | (1) |
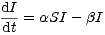 | (2) |
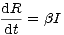 | (3) |
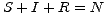 | (4) |
s počátečními podmínkami S(0) = S0 > 0, I(0) = I0 > 0, R(0) = 0, S0 + I0 = N.
Protože veličina R se nevyskytuje v prvních dvou rovnicích systému, je možno uvažovat tyto první dvě rovnice samostatně. Budeme tedy studovat systém
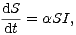 | (5) |
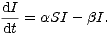 | (6) |
Realistická jsou přitom pouze ta řešení, která splňují S + I < N.
Singulárními body soustavy jsou všechny body přímky I = 0. Soustava má jednu I-nulklinu
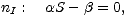
Funkce S(t) je klesající pro všechna t > 0. Funkce I(t) je klesající, pokud 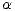 S(t) -
S(t) - 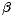 < 0 a
rostoucí, pokud platí opačná nerovnost. I tedy klesá s časem v bodech nalevo od nulkliny nI a roste
napravo od této nulkliny.
< 0 a
rostoucí, pokud platí opačná nerovnost. I tedy klesá s časem v bodech nalevo od nulkliny nI a roste
napravo od této nulkliny.
Pokud platí 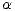 S0 -
S0 - 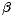 < 0, je funkce I stále klesající a epidemie se tedy nerozšíří, počet
infikovaných bude stále klesat. Tento jev, spočívající v tom, že při dostatečně nízkých hodnotách S0
se epidemie nerozšíří, se nazývá prahový efekt.
< 0, je funkce I stále klesající a epidemie se tedy nerozšíří, počet
infikovaných bude stále klesat. Tento jev, spočívající v tom, že při dostatečně nízkých hodnotách S0
se epidemie nerozšíří, se nazývá prahový efekt.
Pokud platí 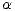 S0 -
S0 - 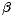 > 0, bude funkce I zpočátku rostoucí a epidemie se bude v populaci šířit.
Toto šíření epidemie bude probíhat až dokud příslušná trajektorie neprotne nulklinu nI, tj až do času
t*, ve kterém platí
> 0, bude funkce I zpočátku rostoucí a epidemie se bude v populaci šířit.
Toto šíření epidemie bude probíhat až dokud příslušná trajektorie neprotne nulklinu nI, tj až do času
t*, ve kterém platí
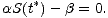 | (7) |
V tomto okamžiku funkce I dosahuje maxima a od tohoto okamžiku bude funkce I klesající.
Funkce S(t) je klesající a nezáporná. Existuje tedy nezáporná konečná limita
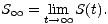 | (8) |
Diferenciální rovnice trajektorií systému je
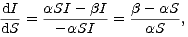 | (9) |
což je rovnice se separovanými proměnnými. Separací proměnných obdržíme
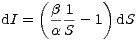 | (10) |
a po integraci
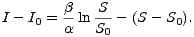 | (11) |
Protože S0 + I0 = N, plyne z této rovnice
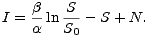 | (12) |
Vzhledem k S + I = N - R dále platí
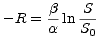 | (13) |
a
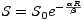 | (14) |
Maximum funkce I nastává v bodě, kde trajektorie protíná I nulklinu, tj. v bodě, kde platí
S = 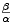 . Dosazením obdržíme
. Dosazením obdržíme
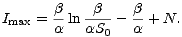 | (15) |
Vzhledem k tomu, že singulární body jsou body přímky I = 0, epidemie skončí tak, že vymizí infikovaní jedinci, tj.
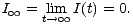 | (16) |
Počet jedinců, kteří se nakazili infekcí, je
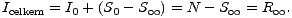 | (17) |
Veličina R je tedy mírou rozsahu epidemie. Dosazením S = N -I -R a limitním přechodem t
je tedy mírou rozsahu epidemie. Dosazením S = N -I -R a limitním přechodem t 
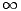 obdržíme
obdržíme
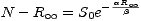
 je tedy řešením rovnice
je tedy řešením rovnice
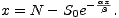
 tím větší (tj. tím blíže N)
čím rychleji exponenciální funkce N -e-
tím větší (tj. tím blíže N)
čím rychleji exponenciální funkce N -e-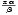 konverguje ke své asymptotě. R
konverguje ke své asymptotě. R je tedy rostoucí funkcí
proměnné
je tedy rostoucí funkcí
proměnné 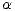 a klesající funkcí proměnné
a klesající funkcí proměnné 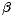 . Aby byl rozsah epidemie co nejmenší, je třeba aby
koeficient
. Aby byl rozsah epidemie co nejmenší, je třeba aby
koeficient 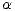 byl co nejmenší (toho lze dosáhnout například snižováním četnosti kontaktů jedinců ze
skupiny I s jedinci ze skupiny S, nebo zvyšováním odolnosti jedinců ze skupiny S) a aby
koeficient
byl co nejmenší (toho lze dosáhnout například snižováním četnosti kontaktů jedinců ze
skupiny I s jedinci ze skupiny S, nebo zvyšováním odolnosti jedinců ze skupiny S) a aby
koeficient 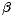 byl co největší (tj. aby proces izolace nemocných jedinců ze skupiny I probíhal co
nejrychleji).
byl co největší (tj. aby proces izolace nemocných jedinců ze skupiny I probíhal co
nejrychleji).