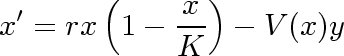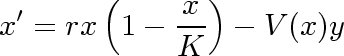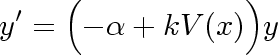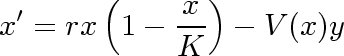
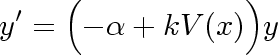
• Můžete měnit hodnoty konstant a trofickou funkci v políčku ” Initialzation ”. Lze sem třeba nakopírovat tučné formule uvedené níže.
• Kliknutím do obrázku (levé tlačítko) zvolíte počáteční podmínku a vykreslí se integrální křivka.
• Je možné měnit interval pro čas i pro velikosti populací.
• Pravým tlačítkem myši a tažením lze definovat výřez pro detail (hlavně v okolí stacionárního bodu nelze dost dobře vidět tvar směrového pole). Zpět se vrátíte prostředním tlačítkem myši.

Možná nastavení políčka Initialzation:

• r=1; K=2; a=1; k=0.8; function V(x)=x — Lotkův-Volterrův model s logistickým růstem kořisti, jeden stabilní uzel
• r=1; K=2; a=0.2; k=0.8; function V(x)=x — Totéž, ale stacionární bod je ohniskem
• r=1; K=2; a=0.2; k=0.8; function V(x)=x/(x+1) — Holling II, limitní cyklus (Max t. nastavit na 500)
• r=1; K=2; a=0.4; k=0.8; function V(x)=x/(x+1) — Holling II, stabilní uzel
• r=1; K=2; a=0.4; k=0.8; function V(x)=(1-exp(-x)) — Holling II, ale jiná funkce;
• r=1; K=3; a=0.2; k=0.2; function V(x)=(if (xĄ1.2) x else 1.2) Holling I;

Další zajímavá nastavení

• Lineární trofická funkce (Lotka-Volterra s logistickým růstem kořisti) a existence úkrytů kořisti (vysvětlete)

  Initialization

  r=1; K=2; a=1; k=0.8; function V(x)=max(x,0)

  dx/dt

  r*x*(1-(x/K))-V(x-0.5)*y

  dy/dt

  (-a+k*V(x-0.5))*y

• Porovnejte křivky s lineární funcí trofickou funkcí V (x) = x a trofickou funkcí typu Holling-I, např.

  Initialization

  r=1; K=2; a=0.7; k=0.8; function V(x)=x

  Initialization

  r=1; K=2; a=0.7; k=0.8; function V(x)=min(x,1)

  Initialization

  r=1; K=2; a=0.7; k=0.8; function V(x)=min(x,0.9)

  Initialization

  r=1; K=2; a=0.7; k=0.8; function V(x)=min(x,0.8) — poslední případ se odlišuje podstatně od případů předchozích. Vysvětlete podstatu rozdílu a snažte se najít příčinu.