R. H. Mac Arthur a E. O. Wilson představili v 60. letech 20. stol. následující teorii dynamické rovnováhy počtu druhů na ostrově.

Předpokládejme, že rychlost kolonizace, tj. počet druhů, které v čase t proniknou na ostrov a úspěšně se zde zabydlí, roste s počtem imigrantů a klesá s počtem druhů, které na ostrově již žijí. První předpoklad je zcela přirozený, druhý vyjadřuje v ekologii obvyklé tvrzení, že komplexnější společenstva organismů jsou stabilnější a lépe odolávají invazi nových druhů. Počet imigrantů klesá s rostoucí vzdáleností ostrova od pevniny, což je opět přirozený předpoklad. Rychlost přibývání druhů lze tedy vyjádřit ve tvaru

---b---, d(N + b)

kde N je počet druhů na ostrově v čase t, d je vzdálenost ostrova od pevniny,

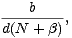
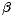je nezáporná a b kladná konstanta.

Předpokládejme, že rychlost vymírání druhů, které v minulosti již úspěšně kolonizovaly ostrov, ale neobstály v konkurenci pozdějších kolonizátorů, roste s klesající rozlohou ostrova a s rostoucím počtem druhů na ostrově. Rychlost vymírání druhů je tedy

N a--, S

kde S je rozloha ostrova a a kladná konstanta. Tento předpoklad je opět přirozený, vzhledem k tomu, že ostrov menší rozlohy má menší nosnou kapacitu. Kromě toho, byl tento předpoklad prověřen i pokusy (viz dále).

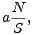
Počet druhů na ostrově rozlohy S ve vzdálenosti d od pevniny tedy vyhovuje diferenciální rovnici

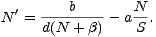b N N '= -------- -a --. d(N + b) S

(1)

Předpokládáme-li, že na počátku byl ostrov neosídlený, připojíme podmínku N(0) = 0.

MODEL

Stacionárním bodem je řešení rovnice

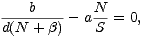
b N d(N-+-b)- a S-= 0,

což po vynásobení faktorem N +

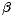a po úpravě vede na kvadratickou rovnici

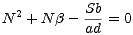
N2 +N b - Sb-= 0 ad

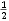
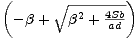s kladným kořenem N₁^* =

a záporným kořenem N₂^* =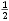

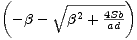. Abychom rozhodli o stabilitě stacionárního bodu N₁^* (bod N₂^* nás nezajímá, protože záporné hodnoty N nemají v našem modelu praktický význam), převedeme rovnici na tvar

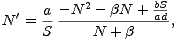2 bS- N '= a--N----bN--+-ad, S N + b

(2)

odkud je zřejmé (načrtněte si parabolu v čitateli zlomku), že stacionární bod N₁^* je stabilní.

Všimněme si, že velikost N₁^* roste s větší rozlohou ostrova S a s menší vzdáleností od pevniny d.

Dále si všimněme, že i když se počet druhů ustálí na konstantní hodnotě, není garantováno, že druhové složení zůstane neměnné. V praxi dojde k tomu, že druhové bohatství (počet druhů) bude konstantní, bude se však měnit složení druhů.

Tyto poznatky byly potvrzeny pokusem s ostrůvky poblíž Floridy. Ostrůvky byly zbaveny chemickou cestou bezobratlých živočichů. Za necelý rok se druhové bohatství díky invazi z pevniny obnovilo. Konkrétní druhové složení však bylo jiné, než před zásahem, a toto druhové složení se neustále měnilo. Ostrůvky poblíž pobřeží hostily více druhů než ty vzdálenější a při dodatečném umělém snížení velikosti některých ostrůvků se jejich druhové bohatství zmenšilo.

V roce 1883 byl opakovanými sopečnými výbuchy téměř zničen život na ostrově u sopky Krakatoa, který leží cca 25 km od Jávy a má rozlohu 20 km². Již v roce 1921 byl tento ostrov osídlen 27 druhy ptáků. Tento počet se v pozdějších letech již neměnil, měnila se pouze druhová skladba. Vzhledem k tomu, že ptáci snadno pronikají na ostrov, se poměrně rychle obnovila jejich rovnováha. 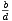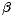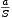Hodnoty koeficientů v tomto případě jsou = 22rok^-1, = 1 a aS- = 0,03rok^-1. Rostlin bylo na tomto ostrově v roce 1934 celkem 271 druhů, tento počet však nadále rostl. Poněkud paradoxně může jevit fakt, že jako první se na ostrově úspěšně uchytili mrchožraví živočichové. Tento jev je však přirozený, uvědomíme-li si, že tito živočichové měli nejhojnější zdroje potravy v podobě mršin živočichů neúspěšně invadujících druhů.

Základy ostrovní ekologie nacházejí jisté uplatnění i při zakládání a udržování rezervací, za účelem zachování druhové pestrosti. Protože, jak ukazuje ostrovní ekologie, omezené kapacity ostrova a nízká migrace způsobí, že přežívá pouze omezený počet druhů, je nutno “ostrovním efektům” co nejvíce zabránit.