5 Obyčejné diferenciální rovnice (úvod)
Obyčejná diferenciální rovnice je matematický vztah mezi neznámou funkcí a jejími derivacemi
Definice 5.1 (obyčejná diferenciální rovnice). Obyčejnou diferenciální rovnicí prvního řádu rozřešenou vzhledem k derivaci (stručně - diferenciální rovnicí (ODR)) s neznámou \( \displaystyle y\) rozumíme rovnici tvaru
| \[ y' = f(x,y) \] | (5.1) |
kde \( \displaystyle f\) je funkce dvou proměnných. Řešením (též integrálem) rovnice na intervalu \( \displaystyle I\) rozumíme každou funkci \( \displaystyle y = y(x)\) , která splňuje identicky (5.1) na \( \displaystyle I\) .
Úloha najít řešení rovnice (5.1), které splňuje zadanou počáteční podmínku
| \[ y(x_{0}) = y_{0} \] | (5.2) |
se nazývá počáteční úloha nebo též Cauchyova úloha. Jejím řešením rozumíme funkci, která splňuje podmínku (5.2) a je na nějakém intervalu obsahujícím bod \( \displaystyle x_{0}\) řešením rovnice (5.1).
Řešení Cauchyovy úlohy nazýváme též partikulárním řešením rovnice (5.1). Graf partikulárního řešení se nazývá integrální křivka.
V souvislosti s diferenciálními rovnicemi nás zajímá především otázka, zda daná rovnice (počáteční úloha) má řešení, na jakém intervalu je toto řešení definováno a zda je určeno jednoznačně. My se budeme navíc zabývat pouze rovnicemi, u nichž lze řešení nalézt analytickou cestou pomocí integrálního počtu.
5.1 Rovnice typu \( \displaystyle y' = f(x)\)
Nejjednodušším příkladem diferenciální rovnice je rovnice tvaru
| \[ y' = f(x). \] | (5.3) |
Z integrálního počtu víme, že tuto rovnici splňuje každá primitivní funkce k funkci \( \displaystyle f\) , tj. že řešením rovnice (5.3) je funkce
| \[ y =\int f(x)\, \mathrm{d}x + C, \] |
kde \( \displaystyle C\) je libovolná konstanta. Takovéto řešení, které obsahuje konstantu, nazýváme obecné řešení rovnice. Toto řešení tedy reprezentuje všechny funkce, vyhovující dané rovnici (je jich zřejmě nekonečně mnoho) Libovolné partikulární řešení získáme z obecného řešení vhodnou volbou konstanty.
Poznámka 5.1 (obecné a partikulární řešení). Podobný princip platí i u dalších diferenciálních rovnic. Funkcí které vyhovují diferenciální rovnici prvního řádu je nekonečně mnoho, zapíšeme-li všechny jedním vzorcem, bude tento vzorec obsahovat jistou konstantu \( \displaystyle C\) . Takový vzorec se nazývá obecné řešení diferenciální rovnice. Každé jednotlivé (partikulární) řešení lze z tohoto vzorce obdržet4 vhodnou volbou konstanty \( \displaystyle C\) .
5.2 Diferenciální rovnice se separovanými proměnnými
V tomto odstavci si uvedeme postup řešení jedné z nejjednodušších diferenciálních rovnic.
Počáteční úloha pro rovnici se separovanými proměnnými nemusí mít vždy jediné řešení. Existují dokonce řešení, které mají porušenu jednoznačnost v každém bodě svého definičního oboru. Tato řešení se nazývají singulární.
Tuto rovnici řešíme separací proměnných následovně:
- (i)
- Má-li rovnice \( \displaystyle g(y) = 0\) řešení \( \displaystyle k_{1}\) , \( \displaystyle k_{2}\) , …, \( \displaystyle k_{n}\) , jsou konstantní funkce \( \displaystyle y = k_{1}\) , \( \displaystyle y = k_{2}\) , …, \( \displaystyle y = k_{n}\) řešeními rovnice. Ostatní řešení jsou nekonstantní a nalezneme je v dalších krocích.
- (ii)
- Dále pracujme jenom na intervalech, kde
\( \displaystyle g(y)\neq 0\) . Formálně
nahradíme derivaci \( \displaystyle y'\)
podílem diferenciálů \( \displaystyle \frac{\, \mathrm{d}y}
{\, \mathrm{d}x}\) :
\[ \frac{\, \mathrm{d}y} {\, \mathrm{d}x} = f(x)g(y) \] - (iii)
- Se zlomkem \( \displaystyle \frac{\, \mathrm{d}y}
{\, \mathrm{d}x}\)
pracujeme ”normálně” jako s podílem dvou výrazů. Násobením a
dělením převedeme rovnici na tvar, který obsahuje na každé
straně pouze jednu proměnnou:
\[ \frac{\, \mathrm{d}y} {g(y)} = f(x)\, \mathrm{d}x. \] - (iv)
- Získanou rovnost zintegrujeme:
\[ \int \frac{\, \mathrm{d}y} {g(y)} =\int f(x)\, \mathrm{d}x + C \] Vlevo je tedy integrál v proměnné \( \displaystyle y\) , vpravo integrál v proměnné \( \displaystyle x\) a na jednu ze stran rovnice přidáme integrační konstantu. Tím obdržíme rovnici, která implicitně zadává obecné řešení rovnice.
- (v)
- Pokud je zadána počáteční podmínka, dosadíme ji do obecného řešení a určíme hodnotu konstanty \( \displaystyle C\) . Tuto dosadíme do obecného řešení a obdržíme řešení partikulární.
- (vi)
- Pokud je to možné, převedeme řešení (obecné nebo partikulární) do explicitního tvaru (”vyjádříme” odsud \( \displaystyle y\) ).
- (vii)
- Pokud je možné některé z konstantních řešení obdržet vhodnou volbou konstanty ve vzorci pro obecné řešení, zahrneme toto konstantní řešení do obecného. Řešení, která není takto možno zahrnout do obecného řešení jsou často singulárními.
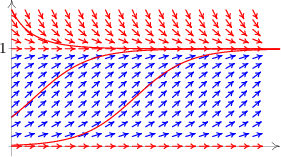
Poznámka 5.2 (geometrický význam diferenciální rovnice). 
Zajímejme
se o to, jak budou vypadat integrální křivky rovnice (5.1). Protože derivace
funkce v bodě udává směrnici tečny ke grafu funkce v tomto bodě,
lze rovnici (5.1) chápat jako předpis, který každému bodu v rovině
přiřadí směrnici tečny k integrální křivce, která
tímto bodem prochází. Sestrojíme-li v dostatečném počtu
(například i náhodně zvolených) bodů \( \displaystyle [x,y]\)
v rovině kratičké úsečky o směrnici \( \displaystyle \varphi (x,y)\) ,
obdržíme směrové pole diferenciální rovnice — systém lineárních
elementů, které jsou tečné k integrálním křivkám. Často
lze ze směrového pole odhadnout tvar integrálních křivek. Protože
se však jedná pouze o odhad tvaru integrálních čar, používáme
tuto metodu jen v případě, kdy nám stačí pouze hrubá
informace o jednotlivých řešeních, nebo v případech kdy selhávají
ostatní dostupné metody.
Počáteční podmínka (5.2) geometricky vyjadřuje skutečnost, že graf příslušného řešení prochází v rovině bodem \( \displaystyle [x_{0},y_{0}]\) . Má-li tato počáteční úloha jediné řešení, neprochází bodem \( \displaystyle [x_{0},y_{0}]\) žádná další křivka. Má-li každá počáteční úloha jediné řešení (což bude pro nás velice častý případ), znamená to, že integrální křivky se nikde neprotínají.
