Rotace vektorového pole
Robert Mařík
2020
Pokud se matematické výrazy nezobrazují korektně, nechejte znovunačíst stránku (Reload, Crtl+R, F5) nebo použijte html verzi prezentace.
Ovládání: Prezentaci je možno posouvat šipkami nebo mezerníkem. Klávesa "S" zmenšuje písmo, "B" zvětšuje (smaller/bigger). Klávesa "C" zobrazí obsah (content). Klávesou "A" se přepíná režim prezentace/html stránka.
Kliknutím na obrázek se obrázek zvětší na vertikální rozměr okna. Pro zavření zvětšeniny klikněte do zašedlého zbytku stránky nebo použijte klávesu "ESC".
Slidy jsou doprovodným materiálem k předáškám. Některá tvrzení platí
pouze za předpokladů dostatečné spojitosti funkcí nebo jejich
derivací. V jednoduchých technických aplikacích bývají tyto
předpoklady splněny a proto je nezmiňujeme. Přesná formulace vět je
v učebním textu a v odborné literatuře.
Totální diferenciál
Definice (totální diferenciál).
Totálním diferenciálem funkce \(z=f(x,y)\) v bodě \((x_0, y_0)\) nazýváme výraz \[ \mathrm{d}f=
\nabla f (x_0,y_0) \cdot (\mathrm{d}x,\mathrm{d}y)=\frac{\partial f (x_0,y_0)}{\partial x}\mathrm{d}x+\frac{\partial f (x_0,y_0)}{\partial y}\mathrm{d}y.
\]
V souvislosti s totálním diferenciálem často vyvstává otázka, zda pro zadané vektorové pole \[\vec F(x,y)=(P(x,y),Q(x,y)),\] existuje skalární funkce \(f\), jejímž gradientem je zadané vektorové pole \(\vec F\). Toto je důležitá otázka ve fyzice, protože umožňuje rozhodnout, ke kterému silovém poli je možno zavést potenciální energii. Funkce \(f\) se v tomto kontextu nazývá skalární potenciál vektorového pole \(\vec F\) nebo také kmenová funkce. Následující věta platí za předpokladu dostatečně hladkých funkcí na otevřené množině.
Věta (nutná a postačující podmínka pro existenci kmenové funkce ve 2D).
Vektor \[\vec F(x,y) = \left( P(x,y) , Q(x,y)\right)\] je gradientem nějaké funkce \(f(x,y)\) právě tehdy když platí \[ \frac{\partial }{\partial y}P(x,y)=\frac{\partial}{\partial x}Q(x,y).\]
Jeden směr implikace v předchozí větě je snadný a plyne hned ze Schwarzovy věty.
Skalární a vektorový součin
Diferenciální operátor divergence jsme poznali v minulé přednášce v souvislosti s difuzní rovnicí. Formálně jde o skalární součin \(\nabla=\left(\frac{\partial }{\partial x},\frac{\partial }{\partial y},\frac{\partial }{\partial z}\right)\) a vektorového pole.
Vektorovým součinem \(\vec a \times \vec b\) vektorů \(\vec a=(a_1,a_2,a_3)\) a \(\vec b=(b_1,b_2,b_3)\) rozumíme vektor \[\vec a\times\vec b=\begin{vmatrix} \vec \imath & \vec \jmath &\vec k \\ a_1&a_2&a_3 \\ b_1& b_2& b_3\end{vmatrix}=(a_2b_3-a_3b_2)\vec\imath+(a_3b_1-a_1b_3)\vec\jmath+(a_1b_2-a_2b_1)\vec k.\]
Rotace
Definice (rotace vektorového pole).
Pro vektorovou funkci tří proměnných \[\vec
F=P\vec \imath+Q\vec \jmath+R\vec k\] definujeme operátor rotace symbolicky vztahem \[
\mathop{\mathrm{rot}} \vec F=\nabla \times \vec F=
\begin{vmatrix}
\vec \imath & \vec \jmath &\vec k\\
\frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z}\\ P &Q &R
\end{vmatrix}.
\]
- Výsledkem rotace je tedy vektorové pole, jehož komponenty jsou \[\nabla \times \vec F=\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)\vec \imath +\left( \frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)\vec \jmath + \left( \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\vec k.\]
- Ve dvourozměrném vektorovém poli doplníme třetí komponentu nulovou. Rotace má potom první dvě komponenty nulové (\(R=\frac{\partial Q}{\partial z}=\frac{\partial P}{\partial z}=0\)) a třetí komponenta je nulová právě tehdy, když k vektorovému poli existuje skalární potenciál.
- Vektorové pole, jehož rotace je rovna nulovému vektoru se nazývá nevírové pole a ve fyzice má důležité postavení - je v něm možno zavést potenciál a potenciální energii.
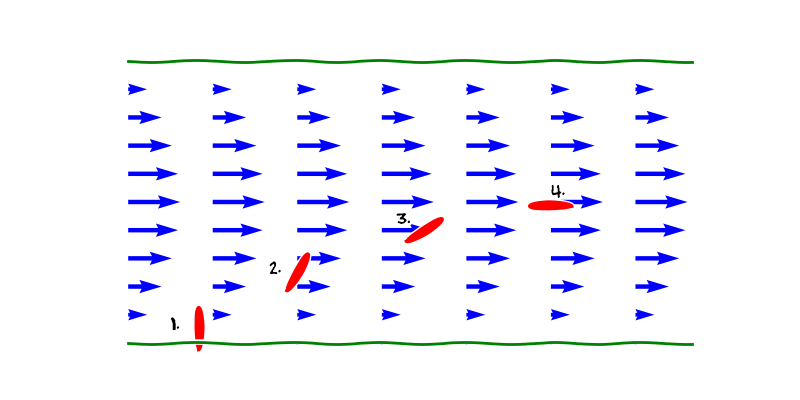
- Představme si vektorové pole charakterizující rychlost proudící tekutiny. Rotace udává, zda má pole tendenci uvést do rotace objekt unášený tímto prouděním. Nejedná se tedy o to, zda se pole točí či netočí jako u víru při vypouštění umyvadla. Příkladem je přímý tok v řece, kdy rychlost u břehu klesá. V důsledku toho se loďka, která odrazí od břehu kolmo stočí po proudu. Mimo středovou osu má pole nenulovou rotaci, i když ve všech bodech míří stejným směrem. Online výpočet.
- Pozor: anglický výraz pro rotaci je “curl”.
Poznámka (linearita rotace).
Rotace zachovává součet a násobení konstantou, tj. pro libovolné vektorové funkce \(\vec F\) a \(\vec G\) a konstantu \(c\) platí \[\nabla \times (\vec F+\vec G)=\nabla \times \vec F +\nabla \times \vec G, \qquad \nabla \times (c\vec F)=c\nabla \cdot \vec F.\]
Zákon šíření chyb - příklad
Kanadský empirický vzorec pro pocitovou teplotu v zimě (wind-chill factor) je \[W(T,v) =
13.12+0.6215 T-11.37 v^{0.16}+0.3965 T v^{0.16},\] kde \(T\) je teplota (ve stupních Celsia) a \(v\) je rychlost větru (v km/hod). Teplota byla změřena \(-11.0\,{}^\circ\!\text{C}\) s chybou \(0.2\,{}^\circ\!\text{C}\) a rychlost \(26 \,\text{km/hod}\) s chybou \(5\,\text{km/hod}\). S využítím zákona šíření chyb určíme, jaký vliv mají nepřesnosti v měření na nepřesnost vypočítané veličiny.
Dosazením do vzorce dostáváme \(W(-11,26)=-20.212\,{}^\circ\!\text{C}\). Derivováním dostáváme \[\begin{aligned}\frac{\partial W}{\partial T}(T,v)&=0.6215+0.3965 v^{0.16},\\
\frac{\partial W}{\partial v}(T,v)&=-11.37\times 0.16 v^{-0.84}+0.3965 \times 0.16 Tv^{-0.84}
\end{aligned}
\] a po dosazení \[\begin{aligned}\frac{\partial W}{\partial T}(-11,26)&=1.289,\\
\frac{\partial W}{\partial v}(-11,26)&=-0.163 \,{}^\circ\!\text{C}\, \text{hod}/\mathrm{km}.
\end{aligned}
\] Za dané teploty a rychlosti větru způsobí nárůst teploty o jeden stupeň nárůst pocitové teploty přibližně o \(1.3\) stupně. Podobně, zesílení větru o jeden kilometr za hodinu způsobí snížení pocitové teploty přibližně o \(0.16\) stupně. Ze zákona šíření chyb dostáváme pro chybu pocitové teploty (dosazováno bez jednotek) \[\Delta W=\sqrt{\left(1.289\times 0.2\right)^2+\left(-0.163\times 5\right)^2}=0.85\,{}^\circ\!\text{C}.\] Pocitová teplota je tedy \(W=-20.2\,{}^\circ\!\text{C}\pm 0.9\,{}^\circ\!\text{C}\).
Online výpočet.